
分析 (1)先判断函数f(x)为定义上的单调递减函数,再用作差比较法证明;
(2)先得出f(2)=3,将原不等式等价为:f[(3-2x)(-x)]>f(2),再运用函数的调调性列不等式组求解.
解答 解:(1)函数f(x)在(0,+∞)单调递减,证明过程如下:
任取x1,x2∈(0,+∞),且x1<x2,所以,0<$\frac{{x}_{1}}{{x}_{2}}$<1,
则f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$•x2)-f(x2)
=f($\frac{{x}_{1}}{{x}_{2}}$)+f(x2)-f(x2)
=f($\frac{{x}_{1}}{{x}_{2}}$)>0,
即f(x1)>f(x2),
∴f(x)在(0,+∞)单调递减;
(2)因为f(4)=f(2)+f(2)=6,所以f(2)=3,
原不等式可写成:f[(3-2x)(-x)]>f(2),
再根据函数的定义域和单调性得$\left\{\begin{array}{l}{3-2x>0}\\{-x>0}\\{(3-2x)•(-x)<2}\end{array}\right.$,
解得,-$\frac{1}{2}$<x<0,
即原不等式的解集为:(-$\frac{1}{2}$,0).
点评 本题主要考查了抽象函数单调性的判断和证明,以及运用抽象函数的单调性解函数不等式,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:高中数学 来源: 题型:解答题
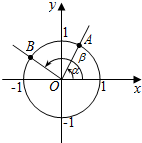 在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.
在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{OM}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OM}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$ | ||
| C. | $\overrightarrow{OM}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | $\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
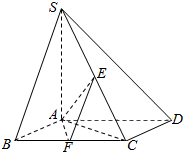 如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com