
分析 (1)设f(x)=ax2+bx+c,求出f(x+1),利用已知条件列出方程组,求解即可.
(2)通过f(x)>2x+m转化为m<x2-3x+1,令g(x)=x2-3x+1,x∈[-1,1],求出g(x)min,然后求解即可.
(3)当$a≤-\frac{1}{2}$时$,-\frac{1}{2}<a<\frac{1}{2}$时,当$a≥\frac{1}{2}$时,分别求解f(x)的最小值即可.
解答 解:(1)设f(x)=ax2+bx+c,则f(x+1)=a(x+1)2+b(x+1)+c.
从而,f(x+1)-f(x)=[a(x+1)2+b(x+1)+c]-(ax2+bx+c)=2ax+a+b,
又f(x+1)-f(x)=2x,
∴$\left\{\begin{array}{l}{2a=2}\\{a+b=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
又f(0)=c=1,∴f(x)=x2-x+1.
(2)由(1)及f(x)>2x+m⇒m<x2-3x+1,
令g(x)=x2-3x+1,x∈[-1,1],则当x∈[-1,1]时,g(x)=x2-3x+1为减函数,
∴当x=1时,g(x)min=g(1)=-1,从而要使不等式m<x2-3x+1恒成立,
则m<-1.
(3)当$a+1≤\frac{1}{2}$,即$a≤-\frac{1}{2}$时,则f(x)在[a,a+1]递减,∴$f{(x)_{min}}=f(a+1)={a^2}+a+1$
当$a<\frac{1}{2}<a+1$,即$,-\frac{1}{2}<a<\frac{1}{2}$时,则f(x)在[a,$\frac{1}{2}$]递减,$[\frac{1}{2},a+1]$递增,
∴$f{(x)_{min}}=f(\frac{1}{2})=\frac{3}{4}$
当$a≥\frac{1}{2}$,时,则f(x)在[a,a+1]递增,
∴$f{(x)_{min}}=f(a)={a^2}-a+1$
∴$g(a)\left\{{\begin{array}{l}{{a^2}+a+1,a≤-\frac{1}{2}}\\{\frac{3}{4},-\frac{1}{2}<a<\frac{1}{2}}\\{{a^2}-a+1,a≥\frac{1}{2}}\end{array}}\right.$.
点评 本题考查二次函数的简单性质的应用,函数的最值的求法以及恒成立的应用,考查转化思想,计算能力.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | $(-1,-\frac{1}{3})$ | D. | $(-∞,-1)∪(-\frac{1}{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
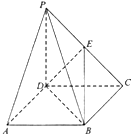 在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=2,点E为PC的中点,连接DE,BD,BE.
在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=2,点E为PC的中点,连接DE,BD,BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com