
分析 (1)由cosC=$\frac{3}{4}$求得sinC,再由正弦定理求得sinA,得到cosA,由余弦定理求得边长AC;
(2)直接由面积公式求得三角形ABC的面积;
(3)展开数量积公式求解.
解答 解:(1)如图,
在△ABC中,由cosC=$\frac{3}{4}$,得sinC=$\sqrt{1-(\frac{3}{4})^{2}}=\frac{\sqrt{7}}{4}$,
由正弦定理得:$\frac{BC}{sinA}=\frac{AB}{sinC}$,∴sinA=$\frac{BC}{AB}•sinC=\frac{1}{\sqrt{2}}×\frac{\sqrt{7}}{4}=\frac{\sqrt{14}}{8}$,
则cosA=$\frac{5\sqrt{2}}{8}$.
∴cosB=-cos(A+C)=-cosAcosC+sinAsinC=-$\frac{5\sqrt{2}}{8}×\frac{3}{4}+\frac{\sqrt{14}}{8}×\frac{\sqrt{7}}{4}$=$-\frac{\sqrt{2}}{4}$.
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cosB}$=$\sqrt{2+1-2×\sqrt{2}×1×(-\frac{\sqrt{2}}{4})}=2$;
(2)${S}_{△ABC}=\frac{1}{2}AB•AC•sinA=\frac{1}{2}×\sqrt{2}×2×\frac{\sqrt{14}}{8}$=$\frac{\sqrt{7}}{4}$;
(3)$\overrightarrow{BC}$•$\overrightarrow{CA}$=$|\overrightarrow{BC}|•|\overrightarrow{CA}|•cos(π-C)$=$1×2×(-\frac{3}{4})=-\frac{3}{2}$.
点评 本题考查平面向量的数量积运算,考查了向量在几何中的应用,训练了三角形的解法,是中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (0,$\frac{5}{2}$) | C. | [$\frac{5}{2}$,4] | D. | [$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
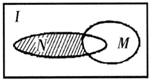 设全集I是实数集R,M={x|x≥3}与N={x|$\frac{x-3}{x-1}$≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|$\frac{x-3}{x-1}$≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com