
分析 对四个命题分别进行判断,即可得出结论.
解答 解:①函数f(x)=cosxsinx=$\frac{1}{2}$sin2x的最大值为$\frac{1}{2}$,不正确;
②命题“?x∈R,x-2≤lgx”的否定是“?x∈R,x-2>lgx”,正确;
③∵△ABC为锐角三角形,∴A+B>$\frac{π}{2}$,∴A>$\frac{π}{2}$-B,∵y=sinx在(0,$\frac{π}{2}$)上是增函数,∴sinA>sin(-B)=cosB 同理可得sinB>cosC,sinC>cosA,∴sinA+sinB+sinC>cosA+cosB+cosCsinA,正确;
④a≤0,函数f(x)=|x2-ax|的零点是a,0,结合二次函数的对称轴,可得函数f(x)=|x2-ax|在区间(0,+∞)内单调递增;若函数f(x)=|x2-ax|在区间(0,+∞)内单调递增,结合二次函数的对称轴,可得$\frac{a}{2}$≤0,∴a≤0,∴“a≤0”是“函数f(x)=|x2-ax|在区间(0,+∞)内单调递增”的充分必要条件,正确.
故答案为:②③④.
点评 本题考查命题的真假判断,考查学生分析解决问题的能力,知识综合性强.


科目:高中数学 来源: 题型:解答题
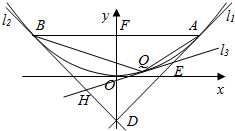 如图,已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为2,点A、点B是抛物线C上的定点,它们到焦点F的距离均为2,且点A位于第一象限.
如图,已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为2,点A、点B是抛物线C上的定点,它们到焦点F的距离均为2,且点A位于第一象限.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 1.5 | 3 | 5 | 6 | 8 | 9 |
| lg x | 4a-2b+c | 2a-b | a+c | 1+a-b-c | 3[1-(a+c)] | 2(2a-b) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com