
分析 (1)函数f(x)=($\frac{1}{3}$)x,则其反函数为y=g(x)=$lo{g}_{\frac{1}{3}}x$.可得g(mx2+2x+1)=-$lo{g}_{3}(m{x}^{2}+2x+1)$,当m≤0时,舍去.当m>0时,g(mx2+2x+1)的定义域为R,可得$\left\{\begin{array}{l}{m>0}\\{△=4-4m<0}\end{array}\right.$,解得m即可得出.
(2)函数y=[f(x)]2-2af(x)+3=$(\frac{1}{3})^{2x}$-2a$(\frac{1}{3})^{x}$+3,x∈[-1,1]时,令$(\frac{1}{3})^{x}$=t∈$[\frac{1}{3},3]$,y=(t-a)2+3-a2=u(t),对称轴t=a.对a与$\frac{1}{3}$,3的大小分类讨论,利用二次函数的单调性即可得出.
(3)存在实数m>n>3,使得函数y=h(x)=-6x+12的定义域为[n,m],值域为[n2,m2],可得$\left\{\begin{array}{l}{-6n+12={m}^{2}}\\{-6m+12={n}^{2}}\end{array}\right.$,解出即可判断出结论.
解答 解:(1)∵函数f(x)=($\frac{1}{3}$)x,则其反函数为y=g(x)=$lo{g}_{\frac{1}{3}}x$=-log3x.
∴g(mx2+2x+1)=-$lo{g}_{3}(m{x}^{2}+2x+1)$,
当m≤0时,g(mx2+2x+1)的定义域不为R,舍去.
当m>0时,g(mx2+2x+1)的定义域为R,则$\left\{\begin{array}{l}{m>0}\\{△=4-4m<0}\end{array}\right.$,解得m>1.
∴实数m的取值范围是(1,+∞).
(2)函数y=[f(x)]2-2af(x)+3=$(\frac{1}{3})^{2x}$-2a$(\frac{1}{3})^{x}$+3,
∵x∈[-1,1]时,令$(\frac{1}{3})^{x}$=t∈$[\frac{1}{3},3]$,
∴y=t2-2at+3=(t-a)2+3-a2=u(t),对称轴t=a.
当a$≤\frac{1}{3}$时,u(t)在t∈$[\frac{1}{3},3]$上单调递增,∴t=$\frac{1}{3}$时,u(t)取得最小值u($\frac{1}{3}$)=$\frac{28-6a}{9}$.
当a≥3时,u(t)在t∈$[\frac{1}{3},3]$上单调递减,∴t=3时,u(t)取得最小值u(3)=12-6a.
当$\frac{1}{3}$<a<3时,u(t)在t∈$[\frac{1}{3},a)$上单调递减,在t∈[a,3]上单调递增,∴t=a时,u(t)取得最小值u(a)=3-a2.
综上可得:最小值h(a)=$\left\{\begin{array}{l}{\frac{28-6a}{9},a≤\frac{1}{3}}\\{-{a}^{2}+3,\frac{1}{3}<a<3}\\{-6a+12,a≥3}\end{array}\right.$.
(3)存在实数m>n>3,使得函数y=h(x)=-6x+12的定义域为[n,m],值域为[n2,m2],
则$\left\{\begin{array}{l}{-6n+12={m}^{2}}\\{-6m+12={n}^{2}}\end{array}\right.$,可得:m2-6m+24=0,由于△=36-96<0,因此上述方程无解.
于是假设不成立,
因此不存在实数m>n>3,使得函数y=h(x)=-6x+12的定义域为[n,m],值域为[n2,m2].
点评 本题考查二次函数的单调性与值域、反函数的求法、一元二次不等式的解集与判别式的关系、换元法,考查了分类讨论方法、推理能力与计算能力,属于难题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,2] | C. | [0,2) | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
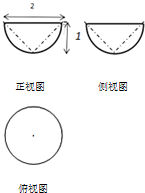
| A. | $\frac{π}{3}$ | B. | $\frac{4}{3}$π | C. | 2π | D. | $\frac{8}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com