
 如图,动圆
如图,动圆 ,1<t<3与椭圆C2:
,1<t<3与椭圆C2: 相交于A,B,C,D四点,点A1,A2分别为C2的左,右顶点.
相交于A,B,C,D四点,点A1,A2分别为C2的左,右顶点. 得
得 ,从而
,从而 =
= ,由此可求矩形ABCD的面积的最大值;
,由此可求矩形ABCD的面积的最大值; ,即可求得直线AA1与直线A2B交点M的轨迹方程.
,即可求得直线AA1与直线A2B交点M的轨迹方程. 得
得 ,从而
,从而 =
= =
=
 ,
, 时,Smax=6
时,Smax=6 时,矩形ABCD的面积取得最大值,最大面积为6;
时,矩形ABCD的面积取得最大值,最大面积为6; ①
① ②
② ③
③ ④
④ (x<-3,y<0)
(x<-3,y<0) (x<-3,y<0).
(x<-3,y<0).

科目:高中数学 来源: 题型:
 (2013•湛江一模)如图,已知点M0(x0,y0)是椭圆C:
(2013•湛江一模)如图,已知点M0(x0,y0)是椭圆C:| y2 |
| 2 |
| y2 |
| a2 |
| x2 |
| b2 |
| y1y |
| a2 |
| x1x |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•辽宁)如图,动圆C1:x2+y2=
(2012•辽宁)如图,动圆C1:x2+y2=| t | 2 |
| x2 |
| 9 |
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(辽宁卷解析版) 题型:解答题
如图,动圆 ,1<t<3,
,1<t<3,
与椭圆 :
: 相交于A,B,C,D四点,点
相交于A,B,C,D四点,点 分别为
分别为 的左,右顶点。
的左,右顶点。
(Ⅰ)当t为何值时,矩形ABCD的面积取得最大值?并求出其最大面积;
(Ⅱ)求直线AA1与直线A2B交点M的轨迹方程。

查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题
 ,1<t<3与椭圆C2:
,1<t<3与椭圆C2: 相交于A,B,C,D四点,点A1,A2分别为C2的左,右顶点。
相交于A,B,C,D四点,点A1,A2分别为C2的左,右顶点。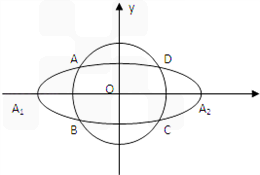
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com