
【题目】设 ![]() ,则对任意实数a、b,若a+b≥0则( )
,则对任意实数a、b,若a+b≥0则( )
A.f(a)+f(b)≤0
B.f(a)+f(b)≥0
C.f(a)﹣f(b)≤0
D.f(a)﹣f(b)≥0
科目:高中数学 来源: 题型:
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(1)根据表中数据,求 ![]() 关于
关于 ![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到 ![]() );
);
(2)若 ![]() 队平均身高为
队平均身高为 ![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测 ![]() 队的平均得分.(精确到个位) 注:回归方程
队的平均得分.(精确到个位) 注:回归方程 ![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,an=  ,n=2,3,4,….
,n=2,3,4,….
(1)求a2 , a3 , a4 , a5的值;
(2)设bn= ![]() +1,n∈N*,求证:数列{bn}是等比数列,并求出其通项公式;
+1,n∈N*,求证:数列{bn}是等比数列,并求出其通项公式;
(3)对任意的m≥2,m∈N*,在数列{an}中是否存在连续的2m项构成等差数列?若存在,写出这2m项,并证明这2m项构成等差数列;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1. 
(1)求证:PA⊥BD;
(2)若∠PCD=45°,求点D到平面PBC的距离h.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为2的等差数列,数列{bn}满足 ![]() ,若n∈N*时,anbn+1﹣bn+1=nbn .
,若n∈N*时,anbn+1﹣bn+1=nbn .
(Ⅰ)求{bn}的通项公式;
(Ⅱ)设cn=anbn , 求{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A1 , A2为椭圆 ![]() =1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1 , A2的三点,直线QA1 , QA2 , OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1 , A2的三点,直线QA1 , QA2 , OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( ) 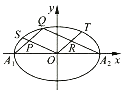
A.5
B.3+ ![]()
C.9
D.14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解市民在购买食物时看营养说明与性别的关系,现在社会上随机询问了100名市民,得到如下2×2列联表:
(1)是否有95%的把握认为:“性别与读营养说明有关系”,并说明理由;
(2)把频率当概率,若从社会上的男性市民中随机抽取3位,记这3位中读营养说明的人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
男性 | 女性 | 总计 | |
读营养说明 | 40 | 20 | 60 |
不读营养说明 | 20 | 20 | 40 |
总计 | 60 | 40 | 100 |
参考公式和数据: ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心为原点O,F(﹣2 ![]() ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( ) 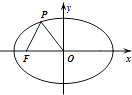
A.![]() =1
=1
B.![]() =1
=1
C.![]() =1
=1
D.![]() =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com