(本题满分为13分).
解:(Ⅰ)f(x)=sin2xcosφ+(2cos
2x-1)•sinφ
=sin2xcosφ+cos2xsinφ=sin(2x+φ),(3分)
由已知得π+φ=kπ+

,k∈Z,又0<φ<π,
∴φ=

,(5分)
∴f(x)=sin(2x+

)=cos2x,
∴ω=2,
则T=

=π.(7分)
(Ⅱ)由已知得x
n=
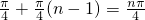
,(8分)
∴f(x
1)+f(x
2)+f(x
3)+f(x
4)=0,(10分)
又∵y=cos

的周期为4,
∴f(x
1)+f(x
2)+…+f(x
2010)+f(x
2011)
=f(x
2009)+f(x
2010)+f(x
2011)
=f(x
1)+f(x
2)+f(x
3)
=cos
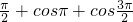
=-1.(13分)
分析:(Ⅰ)把函数解析式的后两项提取sinφ后,利用二倍角的余弦函数公式变形,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据题意及正弦函数单调性得到这个角等于kπ+

,求出φ的值,然后找出ω的值,代入周期公式即可求出函数的最小正周期;
(Ⅱ)由数列

是首项与公差均为

的等差数列,写出此等差数列的通项公式,根据通项公式得到f(x
1)+f(x
2)+f(x
3)+f(x
4)=0,又y=cos

的周期为4,由2011除以4,余数为3,从而得到所求的式子等于f(x
1)+f(x
2)+f(x
3)的值,分别令n=1,2,3求出f(x
1),f(x
2)及f(x
3)的值,即可得到所求式子的值.
点评:本题主要考查两角和与差的正、余弦公式、诱导公式、三角函数的图象和性质、等差数列等基础知识,利用了数形结合思想,培养了学生运算求解的能力,利用三角函数的恒等变形把函数解析式化为一个角的正弦函数是本题第一问的突破点;灵活函数的周期性是解本题第二问的关键.

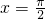 处取得最值.
处取得最值. 是首项与公差均为
是首项与公差均为 的等差数列,求f(x1)+f(x2)+…+f(x2011)的值.
的等差数列,求f(x1)+f(x2)+…+f(x2011)的值. ,k∈Z,又0<φ<π,
,k∈Z,又0<φ<π, ,(5分)
,(5分) )=cos2x,
)=cos2x, =π.(7分)
=π.(7分)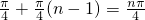 ,(8分)
,(8分) 的周期为4,
的周期为4,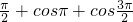
 ,求出φ的值,然后找出ω的值,代入周期公式即可求出函数的最小正周期;
,求出φ的值,然后找出ω的值,代入周期公式即可求出函数的最小正周期; 是首项与公差均为
是首项与公差均为 的等差数列,写出此等差数列的通项公式,根据通项公式得到f(x1)+f(x2)+f(x3)+f(x4)=0,又y=cos
的等差数列,写出此等差数列的通项公式,根据通项公式得到f(x1)+f(x2)+f(x3)+f(x4)=0,又y=cos 的周期为4,由2011除以4,余数为3,从而得到所求的式子等于f(x1)+f(x2)+f(x3)的值,分别令n=1,2,3求出f(x1),f(x2)及f(x3)的值,即可得到所求式子的值.
的周期为4,由2011除以4,余数为3,从而得到所求的式子等于f(x1)+f(x2)+f(x3)的值,分别令n=1,2,3求出f(x1),f(x2)及f(x3)的值,即可得到所求式子的值.

