
| A. | $[\frac{1}{7},1]$ | B. | $[-1,\frac{1}{7}]$ | C. | $(-∞,-\frac{1}{7}]∪[1,+∞)$ | D. | [1,+∞) |
分析 利用导函数的性质研究原函的单调性即可得答案.
解答 解:函数$f(x)=\frac{1}{2}cos2x+3a(sinx-cosx)+(4a-1)x$,
则f′(x)=-sin2x+3a(cosx+sinx)+4a-1.
∵函数f(x)在$[-\frac{π}{2},0]$上单调递增,可得f′($-\frac{π}{2}$)≥0,且f′(0)≥0,
即$\left\{\begin{array}{l}{sinπ+3a(cos\frac{π}{2}-sin\frac{π}{2})+4a-1≥0}\\{sin0+3a(cos0+sin0)+4a-1≥0}\end{array}\right.$,解得:a≥1.
∴得实数a的取值范围为[1,+∞).
故选D.
点评 本题考查了导函数研究原函数的单调性的运用能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
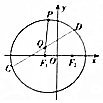 一张半径为4的圆形纸片的圆心为F1,F2是圆内一个定点,且F1F2=2,P是圆上一个动点,把纸片折叠使得F2与P重合,然后抹平纸片,折痕为CD,设CD与半径PF1的交点为Q,当P在圆上运动时,则Q点的轨迹为曲线E,以F1F2所在直线x为轴,F1F2的中垂线为y轴建立平面直角坐标系,如图.
一张半径为4的圆形纸片的圆心为F1,F2是圆内一个定点,且F1F2=2,P是圆上一个动点,把纸片折叠使得F2与P重合,然后抹平纸片,折痕为CD,设CD与半径PF1的交点为Q,当P在圆上运动时,则Q点的轨迹为曲线E,以F1F2所在直线x为轴,F1F2的中垂线为y轴建立平面直角坐标系,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 13 | C. | 17 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com