Question

20．如图，在直角梯形ABCD中，AB∥DC，AD⊥AB，AD=AB=2，DC=4，点M是梯形ABCD内或边界上的一个动点，点N是DC边的中点，则$\overrightarrow{AM}•\overrightarrow{AN}$的最大值是12．

Answer 1

分析 以直线AB为x轴、AD为y轴，建立如图所示直角坐标系，然后求出A、B、C、D、N各点的坐标．设M（x，y），根据数量积的坐标运算公式可得$\overrightarrow{AM}•\overrightarrow{AN}$=2x+2y，设z=2x+2y对应直线l，将直线l进行平移，可得当它经过点C（4，2）时目标函数z达到最大值，由此即可得到的最大值．

解答 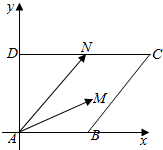解：以AB、AD所在直线分别为x、y，建立如图坐标系，可得
A（0，0），B（2，0），C（4，2），D（0，2），
因此CD中点N坐标为（2，2），
设M（x，y），
∴$\overrightarrow{AM}$=（x，y），$\overrightarrow{AN}$=（2，2），
∴$\overrightarrow{AM}•\overrightarrow{AN}$=2x+2y，
设z=2x+2y对应直线l，
将直线l平移，得当它经过点C（4，2）时，目标函数z达到最大值
∴z=2x+2y的最大值为2×4+2×2=12，
∴$\overrightarrow{AM}•\overrightarrow{AN}$的最大值是12．
故答案为：12．

点评 本题给出直角梯形中的向量，求它们数量积的最大值．着重考查了向量数量积的定义和运用直线平移法求“二元一次型”目标函数的最值等知识，同时考查了学生对向量数量积几何意义灵活应用能力，属于中档题．