
【题目】如图,在四棱锥![]() 中,
中, ![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
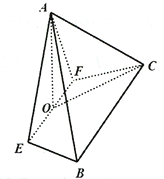
(1)求二面角![]() 的正弦值;
的正弦值;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:
(1)由题意可知![]() ,
, ![]() ,
, ![]() ,据此建立空间直角坐标系,计算可得平面
,据此建立空间直角坐标系,计算可得平面![]() 的法向量为
的法向量为![]() ,且平面
,且平面![]() 的一个法向量为
的一个法向量为![]() ,据此计算可得二面角的正弦值为
,据此计算可得二面角的正弦值为![]() .
.
(2)结合(1)中的空间直角坐标系有![]() ,据此得到关于实数a的方程:
,据此得到关于实数a的方程: ![]() ,解方程有:
,解方程有: ![]() .
.
试题解析:
(1)因为![]() 是等边三角形,
是等边三角形, ![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,
由题设知四边形![]() 是等腰梯形,所以
是等腰梯形,所以![]() ,
,
由![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
建立如图所示空间直角坐标系,
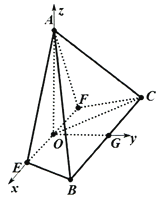
则![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即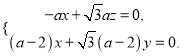
令![]() ,则
,则![]() ,于是
,于是![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,设二面角
,设二面角![]() 为
为![]() ,
,
所以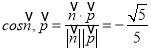 ,
, ![]() ,
,
所以二面角的正弦值为![]() .
.
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() ,
,
由![]() 及
及![]() ,解得
,解得![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (分钟)和销售量
(分钟)和销售量![]() (件)的关系作了统计,得到如下数据:
(件)的关系作了统计,得到如下数据:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)该店主通过作散点图,发现上架时间与销售量线性相关,请你帮助店主求出上架时间与销售量的线性回归方程(保留三位小数),并预测商品上架1000分钟时的销售量;
(2)从这11组数据![]() 中任选2组,设
中任选2组,设![]() 且
且![]() 的数据组数为
的数据组数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:线性回归方程公式: 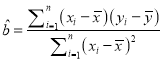 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有2人去淘宝网购物的概率;
(2)求这4个人中去淘宝网购物的人数大于去京东商城购物的人数的概率:
(3)用X,Y分别表示这4个人中去淘宝网购物的人数和去京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC内角A,B,C的对边,函数f(x)=3+2![]() sin xcos x+2cos2x且f(A)=5.
sin xcos x+2cos2x且f(A)=5.
(1)求角A的大小;
(2)若a=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|.
(1)当a=2时,解不等式f(x)>x+1;
(2)若关于x的不等式f(x)+f(-x)< ![]() 有实数解,求m的取值范围.
有实数解,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,则下列函数中有“巧值点”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() 为常数).
为常数).
(1)若直线![]() 与曲线
与曲线![]() 恰好有一个公共点,求实数
恰好有一个公共点,求实数![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com