
| 9 | x |
| 9 |
| x |
| 9 |
| x |
|
| 1 |
| 2 |
| 9 |
| x |
| 9 |
| x |
| 9 |
| x |
| 9 |
| x |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2-1 |
| 1-x2 |
|
| π |
| 2 |
| 2 |
| sinx |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒。当你到达路口时,求不是红灯的概率。(2)已知关于x的一元二次函数![]() 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 在区间[
在区间[![]() 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省攀枝花市高三12月月考文科数学试卷(解析版) 题型:解答题
(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒.当你到达路口时,求不是红灯的概率.
(2)已知关于x的一元二次函数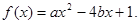 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为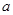 和
和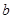 ,求函数
,求函数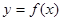 在区间[
在区间[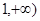 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com