
| y | 2 1 |
| y | 2 2 |
| 1 |
| 2 |
|
| S△FAB |
| S△FBC |
| |AB| |
| |BC| |
| y | 2 1 |
| y | 2 2 |
| (y1-y2)(y1+y2) |
| x1-x2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
|
|
|
| 32+62 |
| 5 |
| 22+42 |
| 5 |
| S△FAB |
| S△FBC |
| |AB| |
| |BC| |
| 3 |
| 2 |


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
 如图,抛物线y=ax2-
如图,抛物线y=ax2-| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
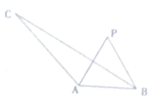 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其他鱼偏高.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm,现从一批数量很大的罗非鱼中随机地抽出15条作为样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后第一位数字为叶)如图所示
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其他鱼偏高.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm,现从一批数量很大的罗非鱼中随机地抽出15条作为样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后第一位数字为叶)如图所示查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| |x+2| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | ||||
an
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com