练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，半圆O的直径MN=2，OA=2，B为半圆上任意一点，以AB为一边作正三角形ABC，问B在什么位置时，四边形OACB面积最大？最大面积是多少？ 

     

     

     

     

    答案：
    解析：

    解：设∠AOB=θ,由余弦定理知AB2=OA2+OB2－2OA·OB·cosθ=5－4cosθ

    ∴S△ABC=θ 

    S△AOB=

    ∴S四边形OACB=

    当θ=时，S四边形OACB最大, 

    最大值为+2

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

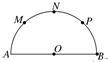    精英家教网如图，AB是半圆O的直径，C，D是弧AB三等分点，M，N是线段AB的三等分点，若OA=6，则
    MD
    •
    NC
    的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，已知AB是半圆O的直径，AB=8，M、N、P是将半圆圆周四等分的三个分点
    （1）从A、B、M、N、P这5个点中任取3个点，求这3个点组成直角三角形的概率；
    （2）在半圆内任取一点S，求三角形SAB的面积大于8
    		2
    的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•成都模拟）如图，AB是半圆O的直径，C、D是弧AB的三等分点，M、N是线段AB的三等分点，若OA=6，则
    MD
    •
    NC
    的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-4-18,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动且总保持PQ=PO,过Q作⊙O的切线交BA的延长线于点C.

    图2-4-18

    (1)当∠QPA=60°时,请你对△QCP的形状作出猜想,并证明;

    (2)当QP⊥AO时,△QCP的形状是___________三角形.

    (3)由(1)、(2)得出的结论,请你进一步猜想,当点P在线段AM上运动到任何位置时△QCP一定是___________三角形.

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年四川省成都市高新区高三（上）12月统考数学试卷（理科）（解析版） 题型：选择题

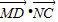    如图，AB是半圆O的直径，C、D是弧AB的三等分点，M、N是线段AB的三等分点，若OA=6，则的值是（ ）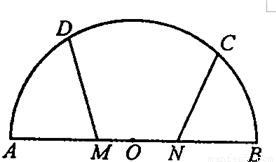

    A．2
    B．5
    C．26
    D．29

    查看答案和解析>>

    同步练习册答案