
在
 中,内角
中,内角 的对边分别为
的对边分别为 .已知
.已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若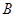 为钝角,
为钝角, ,求
,求 的取值范围.
的取值范围.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往救援,同时把消息告之在甲船的南偏西30°,相距10海里C处的乙船.

(1)求处于C处的乙船和遇险渔船间的距离;
(2)设乙船沿直线CB方向前往B处救援,求∠ACB的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知ΔABC中,满足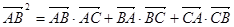 ,a,b,c分别是ΔABC的三边。
,a,b,c分别是ΔABC的三边。
(1)试判定ΔABC的形状,并求sinA+sinB的取值范围。
(2)若不等式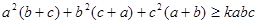 对任意的a,b,c都成立,求实数k的取值范围。
对任意的a,b,c都成立,求实数k的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com