
【题目】函数 ![]() 的定义域为 , 值域为 .
的定义域为 , 值域为 .
【答案】(﹣∞,0)∪(0,+∞);(﹣∞,﹣1)∪(1,+∞)
【解析】解:由题意,函数y=f(x)= ![]() =
= ![]() ,分母不为0,∴102x﹣1≠0,
,分母不为0,∴102x﹣1≠0,
∴x≠0;
∴函数f(x)的定义域为(﹣∞,0)∪(0,+∞);
令y= ![]() ,
,
∴y(102x﹣1)=102x+1,
∴102x(y﹣1)=y+1,
∴ ![]() ,
,
∴x= ![]() ;
;
由对数的定义知, ![]() ,解得,y<﹣1或y>1;
,解得,y<﹣1或y>1;
【考点精析】本题主要考查了函数的定义域及其求法和函数的值域的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第六组比第七组多1人,第一组和第八组人数相同.
(I)求第六组、第七组的频率并补充完整频率分布直方图;
(Ⅱ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x﹣y|≤5的事件概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
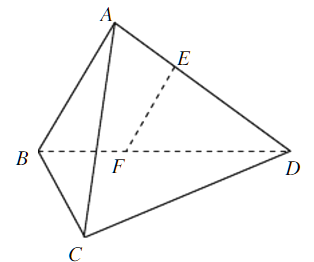
【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四面体ABCD中, ![]() 是
是![]() 的中心,
的中心, ![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() .
.
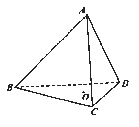
(1)若![]() 平面
平面![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,正四面体ABCD的棱长为
,正四面体ABCD的棱长为![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角余弦值.
所成的角余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量70后、80后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从70后和80后的员工中随机调查了100位,得到数据如下表:
愿意被外派 | 不愿意被外派 | 合计 | |
70后 | 20 | 20 | 40 |
80后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
(Ⅰ)根据调查的数据,是否有90%以上的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(Ⅱ)该公司举行参观驻海外分支机构的交流体验活动,拟安排4名参与调查的70后员工参加.70后员工中有愿意被外派的3人和不愿意被外派的3人报名参加,现采用随机抽样方法从报名的员工中选4人,求选到愿意被外派人数不少于不愿意被外派人数的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣1)2=2经过椭圆Γ: ![]() +
+ ![]() =1(a>b>0)的右焦点F和上顶点B.
=1(a>b>0)的右焦点F和上顶点B.
(1)求椭圆Γ的方程;
(2)过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点,求 ![]()
![]() 的最大值.
的最大值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C的焦点与椭圆 ![]() =1的焦点相同,且渐近线方程为y=±
=1的焦点相同,且渐近线方程为y=± ![]() x.
x.
(1)求双曲线C的标准方程;
(2)设F1为双曲线的左焦点,P为双曲线C的右支上一点,且线段PF1的中点在y轴上,求△PF1F2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
某电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(I)用![]() ,
,![]() 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(II)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com