
����Ŀ������С������13�֣�
ij����̨���ż�����������������ÿ�β���������ʱ����Ҫ���Ź��.��֪ÿ�β��żס�������������ʱ�������粥��ʱ������沥��ʱ���������˴����±���ʾ��
�����粥��ʱ�������ӣ� | ��沥��ʱ���������� | �����˴������� | |
�� | 70 | 5 | 60 |
�� | 60 | 5 | 25 |
��֪����̨ÿ�ܰ��ż�������������ܲ���ʱ�䲻����600���ӣ������ܲ���ʱ�䲻����30���ӣ��Ҽ������粥�ŵĴ����������������粥�Ŵ�����2��.�ֱ���![]() ��
��![]() ��ʾÿ�ܼƻ������ļ���������������Ĵ���.
��ʾÿ�ܼƻ������ļ���������������Ĵ���.
��I����![]() ��
��![]() �г�������Ŀ��������ѧ��ϵʽ����������Ӧ��ƽ��������
�г�������Ŀ��������ѧ��ϵʽ����������Ӧ��ƽ��������
��II���ʵ���̨ÿ�ܲ�����������������������ٴ�������ʹ�����˴������
���𰸡�(1)��������2������̨ÿ�ܲ�����������6�Ρ���������3��ʱ����ʹ�������˴����.
���������������⣺����֪��![]() �������ѧ��ϵʽΪ
�������ѧ��ϵʽΪ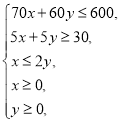 ��
��
�ö�Ԫһ�β���ʽ������ʾ��ƽ������Ϊͼ1�е���Ӱ���֣�
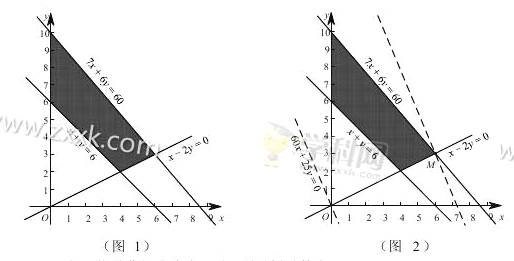
�������⣺���������˴�Ϊ![]() ����Ŀ�꺯��Ϊ
����Ŀ�꺯��Ϊ![]() .
.
����![]() ����������Ϊ
����������Ϊ![]() ������б��Ϊ
������б��Ϊ![]() ����
����![]() �仯��һ��ƽ��ֱ��.
�仯��һ��ƽ��ֱ��.![]() Ϊֱ����
Ϊֱ����![]() ���ϵĽؾ࣬��
���ϵĽؾ࣬��![]() ȡ�����ֵʱ��
ȡ�����ֵʱ��![]() ��ֵ���.����Ϊ
��ֵ���.����Ϊ![]() ����Լ��������������ͼ2��֪����ֱ��
����Լ��������������ͼ2��֪����ֱ��![]() �����������ϵĵ�Mʱ���ؾ�
�����������ϵĵ�Mʱ���ؾ�![]() ���
���![]() ���.
���.
�ⷽ����![]() �õ�M������Ϊ
�õ�M������Ϊ![]() .
.
���ԣ�����̨ÿ�ܲ�����������6�Ρ���������3��ʱ����ʹ�������˴����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ��
��![]() �����ϡ�����������ֱ�Ϊ
�����ϡ�����������ֱ�Ϊ![]() ��
�� ![]() ����
����![]() ��ֱ�߽���Բ��
��ֱ�߽���Բ��![]() ��
�� ![]() ���㣬��
���㣬��![]() ���ܳ�Ϊ8����Բ
���ܳ�Ϊ8����Բ![]() ��������Ϊ
��������Ϊ![]() .
.
��1������Բ![]() �ı����̣�
�ı����̣�
��2����֪![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() ��
�� ![]() ����Բ
����Բ![]() ���ҽ���һ�������㣬��
���ҽ���һ�������㣬��![]() ��
�� ![]() ��ֱ��
��ֱ��![]() �ϵ����㣬��
�ϵ����㣬��![]() ��
�� ![]() �����ı���
�����ı���![]() ���
���![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B��C������ֱ�ΪA��4��0����B��0��4����C��3cos����3sin������
��1�������ʣ����У�0������| ![]() |=|
|=| ![]() |����Ǧ��Ĵ�С��
|����Ǧ��Ĵ�С��
��2���� ![]() ��
�� ![]() ����
���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵĺ���f��x����f�䣨x�����䵼����������f��x��+f�䣨x����2��ef��1��=2e+4����ʽexf��x����4+2ex������eΪ��Ȼ�����ĵ������Ľ⼯Ϊ�� ��
A.��1��+�ޣ�
B.�����ޣ�0���ȣ�1��+�ޣ�
C.�����ޣ�0���ȣ�0��+�ޣ�
D.�����ޣ�1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={��x��y��|x2+��y+1��2��1}��B={��x��y��| ![]() x+y=4m}������P��A��B=������q��ֱ��
x+y=4m}������P��A��B=������q��ֱ�� ![]() +
+ ![]() =1�����������ϵĽؾ�Ϊ����
=1�����������ϵĽؾ�Ϊ����
��1��������PΪ�����⣬��ʵ��m��ȡֵ��Χ��
��2������p��q��Ϊ�棬��p��q��Ϊ�٣���ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������A��B��C������ͬ��������ͬһ��Ʒ����������λ�����������ʾ���ʼ���Ա�÷ֲ�����ķ�������Щ��Ʒ�й���ȡ6����Ʒ���м�⣮
���� | A | B | C |
���� | 50 | 150 | 100 |
��1������6����Ʒ������A��B��C�������Ʒ��������
��2��������6����Ʒ�������ȡ2�����н�һ����⣬����2����Ʒ������ͬ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�ǵ��������Σ�BA=BC��DC��ƽ��ABC��AE��DC����AC=2��BE��AD���� �� 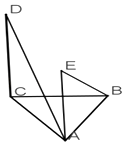
A.AB+BC�����ֵ
B.AB+BC����Сֵ
C.AE+DC�����ֵ
D.AE+DC����Сֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com