
已知圆M经过双曲线S: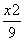 -
-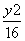 =1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )
=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )
A.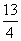 或
或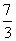 B.
B.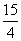 或
或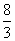 C.
C.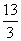 D.
D.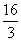
科目:高中数学 来源: 题型:
已知向量a=(sin x,2cos x),b=(2sin x,sin x),设函数f(x)=a·b.
(1)求f(x)的单调递增区间;
(2)若将f(x)的图象向左平移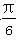 个单位,得到函数g(x)的图象,求函数g(x)在区间
个单位,得到函数g(x)的图象,求函数g(x)在区间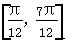 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1,a2的等差中项,a2为b2,b3的等差中项.
(1)求数列{an}与{bn}的通项公式;
(2)记cn=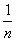 (a1+a2+…+an)(b1+b2+…+bn),求数列{cn}的前n项和Sn.
(a1+a2+…+an)(b1+b2+…+bn),求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x+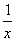 (x>0),以点(n,f(n))为切点作函数图象的切线ln(n∈N*),直线x=n+1与函数y=f(x)图象及切线ln分别相交于An,Bn,记an=|AnBn|.
(x>0),以点(n,f(n))为切点作函数图象的切线ln(n∈N*),直线x=n+1与函数y=f(x)图象及切线ln分别相交于An,Bn,记an=|AnBn|.
(1)求切线ln的方程及数列{an}的通项;
(2)设数列{nan}的前n项和为Sn,求证:Sn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)的定义域为D,若f(x)满足下面两个条件则称f(x)为闭函数:①f(x)是D上的单调函数;②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b].现已知f(x)=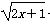 +k为闭函数,则k的取值范围是( )
+k为闭函数,则k的取值范围是( )
A.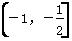 B.(-∞,1)
B.(-∞,1)
C.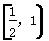 D.(-1,+∞)
D.(-1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.

(1)若直线l的斜率为1,求|AB|的值;
(2)求△PAB的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}(n∈N*)是首项为1的等比数列,设bn=an+2n,若数列{bn}也是等比数列,
则b1+b2+b3= ( )
A.9 B.21 C.42 D.45
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线ax+y+2=0及两点P(-2,1)、Q(3,2),若直线与线段PQ相交,则a的取值范围是 ( )
A、a≤-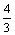 或a≥
或a≥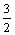 B、a≤-
B、a≤-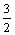 或a≥
或a≥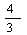 C、-
C、-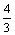 ≤a≤
≤a≤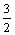 D、-
D、-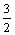 ≤a
≤a ≤
≤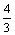
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com