
【题目】已知动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦长为
轴上截得的弦长为![]() .
.
(1)求动圆![]() 的圆心点
的圆心点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)过点![]() 的动直线与曲线
的动直线与曲线![]() 交于
交于![]() 两点,平面内是否存在定点
两点,平面内是否存在定点![]() ,使得直线
,使得直线![]() 分别交
分别交![]() 于
于![]() 两点,使得直线
两点,使得直线![]() 的斜率
的斜率![]() ,满足
,满足![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:

根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记![]() 为选出的两人中甲大学的人数,求
为选出的两人中甲大学的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值![]() 与
与![]() 的大小,及方差
的大小,及方差![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .(Ⅰ)求点
.(Ⅰ)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(Ⅱ)过![]() 的直线
的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,过
两点,过![]() 作与
作与![]() 垂直的直线
垂直的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在小明的婚礼上,为了活跃气氛,主持人邀请10位客人做一个游戏.第一轮游戏中,主持人将标有数字1,2,…,10的十张相同的卡片放入一个不透明箱子中,让客人依次去摸,摸到数字6,7,…,10的客人留下,其余的淘汰,第二轮放入1,2,…,5五张卡片,让留下的客人依次去摸,摸到数字3,4,5的客人留下,第三轮放入1,2,3三张卡片,让留下的客人依次去摸,摸到数字2,3的客人留下,同样第四轮淘汰一位,最后留下的客人获得小明准备的礼物.已知客人甲参加了该游戏.
(1)求甲拿到礼物的概率;
(2)设![]() 表示甲参加游戏的轮数,求
表示甲参加游戏的轮数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,
轴不重合, ![]() 交圆
交圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设![]() ,过点
,过点![]() 作直线
作直线![]() ,交点
,交点![]() 的轨迹于
的轨迹于![]() 两点 (异于
两点 (异于![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
D. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
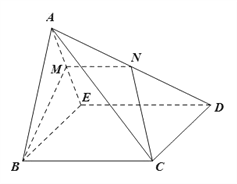
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com