
【题目】在小明的婚礼上,为了活跃气氛,主持人邀请10位客人做一个游戏.第一轮游戏中,主持人将标有数字1,2,…,10的十张相同的卡片放入一个不透明箱子中,让客人依次去摸,摸到数字6,7,…,10的客人留下,其余的淘汰,第二轮放入1,2,…,5五张卡片,让留下的客人依次去摸,摸到数字3,4,5的客人留下,第三轮放入1,2,3三张卡片,让留下的客人依次去摸,摸到数字2,3的客人留下,同样第四轮淘汰一位,最后留下的客人获得小明准备的礼物.已知客人甲参加了该游戏.
(1)求甲拿到礼物的概率;
(2)设![]() 表示甲参加游戏的轮数,求
表示甲参加游戏的轮数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个实数组成的
个实数组成的![]() 行
行![]() 列的数表,满足:每个数的绝对值不大于
列的数表,满足:每个数的绝对值不大于![]() ,且所有数的和为零,记
,且所有数的和为零,记![]() 为所有这样的数表组成的集合,对于
为所有这样的数表组成的集合,对于![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和(
行各数之和(![]() 剟
剟![]()
![]() ),
),![]() 为
为![]() 的第
的第![]() 列各数之和(
列各数之和(![]() 剟
剟![]() ),记
),记![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 中的最小值.
中的最小值.
(![]() )对如下数表
)对如下数表![]() ,求
,求![]() 的值.
的值.
|
|
|
|
|
|
(![]() )设数表
)设数表![]() 形如:
形如:
|
|
|
|
|
|
求![]() 的最大值.
的最大值.
(![]() )给定正整数
)给定正整数![]() ,对于所有的
,对于所有的![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
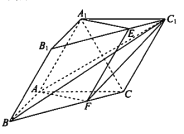
(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)记四棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦长为
轴上截得的弦长为![]() .
.
(1)求动圆![]() 的圆心点
的圆心点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)过点![]() 的动直线与曲线
的动直线与曲线![]() 交于
交于![]() 两点,平面内是否存在定点
两点,平面内是否存在定点![]() ,使得直线
,使得直线![]() 分别交
分别交![]() 于
于![]() 两点,使得直线
两点,使得直线![]() 的斜率
的斜率![]() ,满足
,满足![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=e2x-aln x.
(1)讨论f(x)的导函数f′(x)零点的个数;
(2)证明:当a>0时,f(x)≥2a+aln![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若曲线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且在点
,且在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,求实数
,求实数![]() 的值;
的值;
(2)记![]() 的导函数为
的导函数为![]() ,
, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() , 平面
, 平面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 是
是![]() 中点.
中点.
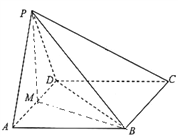
(1)求证:平面![]() 平面
平面![]() ;
;
(2)证明: ![]() , 且
, 且![]() 与
与![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,令
,令![]() .
.
(Ⅰ)写出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在数列![]() ,使得
,使得![]() ?若存在,求出数列
?若存在,求出数列![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com