
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() , 平面
, 平面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 是
是![]() 中点.
中点.
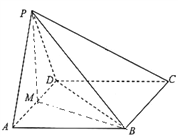
(1)求证:平面![]() 平面
平面![]() ;
;
(2)证明: ![]() , 且
, 且![]() 与
与![]() 的面积相等.
的面积相等.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由正三角形性质得PM⊥AD,再根据面面垂直性质定理得PM⊥底面ABCD,即得PM⊥BM,利用勾股定理得BM⊥AD,最后根据线面垂直判定定理得BM⊥平面PAD,由面面垂直判定定理得结论(2)利用余弦定理求两角余弦值,结合余弦函数单调性确定两角大小,根据三角形面积公式计算面积,可证相等
试题解析: 解:(1) ![]() △PAD是边长为2的等边三角形, M是AD中点
△PAD是边长为2的等边三角形, M是AD中点
![]()
![]() PM⊥AD, PM
PM⊥AD, PM![]() 平面PAD
平面PAD
又平面PAD⊥底面ABCD PM⊥底面ABCD
平面PAD∩底面ABCD=AD
又![]() BM
BM![]() 底面ABCD,
底面ABCD, ![]() PM⊥BM, △PMB是直角三角形
PM⊥BM, △PMB是直角三角形
在等边△PAD中,PM=![]() ,又PB=
,又PB=![]() , MB=
, MB=![]()
∠BAD=60○, 在△ABM中, 由余弦定理:MB2 = AM2+AB2-2AM×AB×cos60○
得:AB2 - AB -2=0, 即AB=2, ![]() △ABD也是等边三角形,
△ABD也是等边三角形,
![]()
![]() BM⊥AD
BM⊥AD
![]() 平面PAD∩底面ABCD=AD BM⊥平面PAD
平面PAD∩底面ABCD=AD BM⊥平面PAD
BM![]() 底面ABCD BM
底面ABCD BM![]() 平面PMB
平面PMB ![]() 平面PMB⊥平面PAD
平面PMB⊥平面PAD
(Ⅱ)由(Ⅰ)知底面ABCD是菱形. 连接CM, 在△DMC中,∠MDC=120○,
由余弦定理:MC2 = MD2+CD2-2MD×CD×cos120○ =12+ 22-2×1×2×![]() =7
=7
得: MC=![]() , 在直角形△PMC中, :PC2 =PM2+MC2=
, 在直角形△PMC中, :PC2 =PM2+MC2=![]()
在△PDC中,由余弦定理: 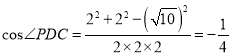
在△PAB中,由余弦定理: 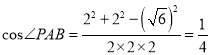
![]()
![]() ,
, ![]() ,余弦函数在
,余弦函数在![]() 是减函数
是减函数
![]() ∠PDC >∠PAB,
∠PDC >∠PAB,
而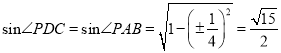 ,
,
![]() ,即△PDC与△PAB面积相等.
,即△PDC与△PAB面积相等.
(注:没有通过计算出面积,能够说明面积相等原因的,仍然是满分)


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() ,且经过点
,且经过点![]() ,
, ![]() 轴.
轴.
(1)求椭圆![]() 的方程;
的方程;
(2)设过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两不同点,在椭圆
两不同点,在椭圆![]() 上是否存在一点
上是否存在一点![]() ,使四边形
,使四边形![]() 为平行四边形?若存在,求出直线
为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在小明的婚礼上,为了活跃气氛,主持人邀请10位客人做一个游戏.第一轮游戏中,主持人将标有数字1,2,…,10的十张相同的卡片放入一个不透明箱子中,让客人依次去摸,摸到数字6,7,…,10的客人留下,其余的淘汰,第二轮放入1,2,…,5五张卡片,让留下的客人依次去摸,摸到数字3,4,5的客人留下,第三轮放入1,2,3三张卡片,让留下的客人依次去摸,摸到数字2,3的客人留下,同样第四轮淘汰一位,最后留下的客人获得小明准备的礼物.已知客人甲参加了该游戏.
(1)求甲拿到礼物的概率;
(2)设![]() 表示甲参加游戏的轮数,求
表示甲参加游戏的轮数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为![]() 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为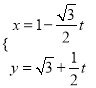 (
(![]() 为参数).
为参数).
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
, ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
D. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
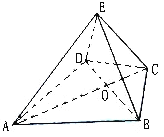
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为45°,求二面角
所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
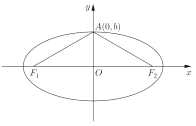
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,设点
,设点![]() ,在
,在![]() 中,
中, ![]() ,周长为
,周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(3)记第(2)问所求的定点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的一个动点,试根据
上的一个动点,试根据![]() 面积
面积![]() 的不同取值范围,讨论
的不同取值范围,讨论![]() 存在的个数,并说明理由.
存在的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右有顶点分别是
的左、右有顶点分别是![]() 、
、![]() ,上顶点是
,上顶点是![]() ,圆
,圆![]() :
:![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离是
的距离是![]() ,且椭圆的右焦点与抛物线
,且椭圆的右焦点与抛物线![]() 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)平行于![]() 轴的动直线与椭圆和圆在第一象限内的交点分别为
轴的动直线与椭圆和圆在第一象限内的交点分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,
,![]() .试判断
.试判断![]() 是否为定值,若是,证明你的结论.若不是,举反例说明.
是否为定值,若是,证明你的结论.若不是,举反例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com