
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 由f(x)在点P(x0,f(x0))处的切线方程为l:y=g(x),得到g(x)的表达式,代入f(x)-g(x),求其导函数,利用0<x0<$\frac{\sqrt{2}}{2}$时,在(x0,$\frac{1}{2{x}_{0}}$)上m′(x)<0,m(x)在此区间上单调递增,当x0>$\frac{\sqrt{2}}{2}$时,在($\frac{1}{2{x}_{0}}$,x0)上m′(x)<0,mφ(x)在此区间上单调递减,可得x0的值.
解答 解:f(x)=x2-x+lnx的导数为f′(x)=2x-1+$\frac{1}{x}$,
由函数f(x)在点P(x0,f(x0))处的切线方程为l:y=g(x),
则g(x)-(x02-x0+lnx0)=(2x0-1+$\frac{1}{{x}_{0}}$)(x-x0),
即g(x)=(2x0-1+$\frac{1}{{x}_{0}}$)(x-x0)+x02-x0+lnx0,
令m(x)=f(x)-g(x)=x2-x+lnx-(2x0-1+$\frac{1}{{x}_{0}}$)(x-x0)-x02+x0-lnx0.
则m(x0)=0.
m′(x)=2x-1+$\frac{1}{x}$-(2x0-1+$\frac{1}{{x}_{0}}$)=$\frac{2}{x}$(x-x0)(x-$\frac{1}{2{x}_{0}}$),
若0<x0<$\frac{\sqrt{2}}{2}$时,m(x)在(x0,$\frac{1}{2{x}_{0}}$)上m′(x)<0,m(x)在此区间上单调递减,
当x∈(x0,$\frac{1}{2{x}_{0}}$)时,m(x)<m(x0)=0,此时$\frac{m(x)}{x-{x}_{0}}$<0不合题意;
若x0>$\frac{\sqrt{2}}{2}$时,m(x)在($\frac{1}{2{x}_{0}}$,x0)上m′(x)<0,m(x)在此区间上单调递减,
当x∈($\frac{1}{2{x}_{0}}$,x0)时,m(x)>m(x0)=0,此时$\frac{m(x)}{x-{x}_{0}}$<0不合题意;
当x0=$\frac{\sqrt{2}}{2}$时,m′(x)=$\frac{2}{x}$(x-$\frac{\sqrt{2}}{2}$)2≥0,m(x)在(0,+∞)递增,
当x>x0时,m(x)>m(x0)=0,此时$\frac{m(x)}{x-{x}_{0}}$>0;
当x<x0时,m(x)<m(x0)=0,此时$\frac{m(x)}{x-{x}_{0}}$>0,成立.
故选:B.
点评 本题考查了利用导数研究过曲线上某点处的切线方程,正确理解导数的几何意义及熟练掌握利用导数研究函数的单调性是解题的关键,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
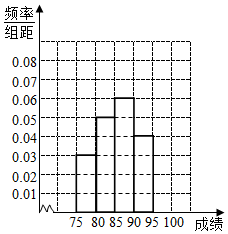 将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.
将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:填空题
如图,在长方体ABCD—A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1—ABD1的体积___________cm3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com