
(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
(1)从第4年开始获取纯利润。
(2)两种方案获利一样多,而方案(1)时间比较短,所以选择方案(1)。
解析试题分析:(1)设第n年获取利润为y万元,n年共收入租金30n万元.付出装修费共 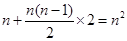 ,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.
,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.
(2)①纯利润总和最大时,以10万元出售,利用二次函数的性质求出最大利润,方案②利用基本不等式进行求解,当两种方案获利一样多,就看时间哪个方案短就选择哪个..
(1)设第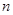 年获取利润为
年获取利润为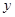 万元。………………1分
万元。………………1分 年共收租金30
年共收租金30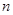 万元,付出装修费构成一个以1为首项,2为公差的等差数列,
万元,付出装修费构成一个以1为首项,2为公差的等差数列,
共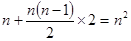 …………………2分
…………………2分
因此利润 令
令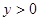 ……………4分
……………4分
解得 ……………5分
……………5分
所以从第4年开始获取纯利润。………………6分
(2)年平均利润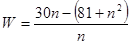 ………………8分
………………8分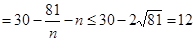 ………………9分
………………9分
(当且仅当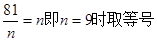 )所以9年后共获利润:154万元。……………10分
)所以9年后共获利润:154万元。……………10分
利润
所以15年后共获利润:144+10=154万元……………………11分
两种方案获利一样多,而方案(1)时间比较短,所以选择方案(1)。…………………12分
考点:函数的模型及其应用。
点评:本题是函数模型选取问题,在直接比较不能凑效的前提下可考虑作差法比较.


科目:高中数学 来源: 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用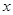 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本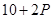 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为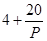 元/万件.
元/万件.
(Ⅰ)将该产品的利润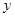 万元表示为促销费用
万元表示为促销费用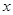 万元的函数;
万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100
元,已知总收入满足函数: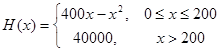 ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(1)将利润表示为月产量的函数(用 表示);
表示);
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?(总收入=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
某市居民生活用水收费标准如下:
用水量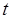 (吨) (吨) | 每吨收费标准(元) |
不超过 吨部分 吨部分 | 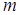 |
超过 吨不超过 吨不超过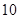 吨部分 吨部分 | 3 |
超过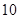 吨部分 吨部分 | 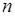 |
 吨,缴纳的水费为
吨,缴纳的水费为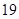 元;二月份用水量为
元;二月份用水量为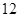 吨,缴纳的水费为
吨,缴纳的水费为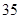 元.设某用户月用水量为
元.设某用户月用水量为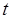 吨,交纳的水费为
吨,交纳的水费为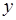 元.
元.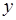 关于
关于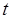 的函数关系式;
的函数关系式;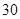 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用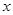 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本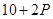 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为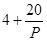 元.
元.
(Ⅰ)将该产品的利润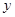 万元表示为促销费用
万元表示为促销费用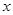 万元的函数(利润=总售价-成本-促销费);
万元的函数(利润=总售价-成本-促销费);
(Ⅱ)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com