
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
(1)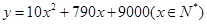 ;(2) 30层.
;(2) 30层.
解析试题分析:(1)由已知,写字楼最下面一层的总建筑费用为: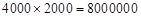 (元)
(元)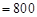 (万元),
(万元),
从第二层开始,每层的建筑总费用比其下面一层多: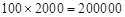 (元)
(元) (万元),
(万元),
写字楼从下到上各层的总建筑费用构成以800为首项,20 为公差的等差数列
所以函数表达式为: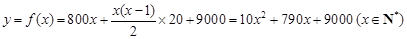 ;…………8分
;…………8分
(2)由(1)知写字楼每平方米平均开发费用为: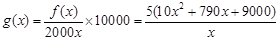
 (元)
(元)
当且仅当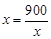 ,即
,即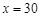 时等号成立.
时等号成立.
答:该写字楼建为30层时,每平方米平均开发费用最低. …………16分
考点:本题考查数列的应用;函数模型的选择与应用;基本不等式在最值问题中的应用.
点评:本题考查等差数列模型的构建、基本不等式的运用及利用数学知识解决实际问题的能力,属于中档题。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)定义在实数R上的函数y= f(x)是偶函数,当x≥0时,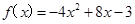 .
.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数
(1)若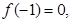 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的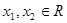 ,且
,且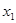 <
<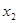 ,
,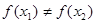 (
(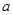 >0),试证明:
>0),试证明: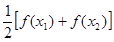 >
>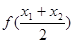 成立。
成立。
(3)是否存在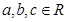 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意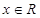 ,
, ,且
,且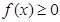 ②对任意的
②对任意的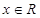 ,都有
,都有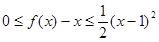 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品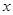 (百台),其总成本为
(百台),其总成本为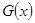 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入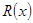 (万元)满足
(万元)满足 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出函数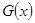 的解析式;
的解析式;
(2)写出利润函数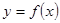 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
(3)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com