
已知二次函数
(1)若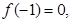 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的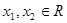 ,且
,且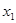 <
<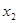 ,
,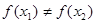 (
(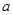 >0),试证明:
>0),试证明: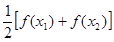 >
>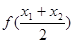 成立。
成立。
(3)是否存在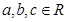 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意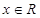 ,
, ,且
,且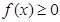 ②对任意的
②对任意的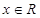 ,都有
,都有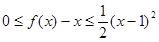 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(1) 零点为1个或2个;(2)见解析;(3)  。
。
解析试题分析:(1)∵f(-1)=0,∴a-b+c=0即b=a+c,故△=b2-4ac=(a+c)2-4ac=(a-c)2,
当a=c时,△=0,函数f(x)有一个零点;当a≠c时,△>0,函数f(x)有两个零点.
(2)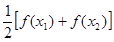 -
-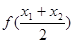 =
=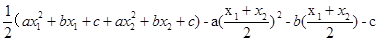
=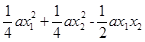 =
=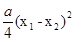
因为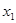 <
<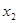 ,
,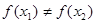 (
(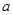 >0)所以
>0)所以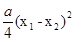 >0,即
>0,即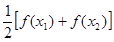 -
-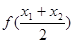 >0,
>0,
所以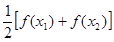 >
>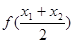 成立。
成立。
(3)假设存在a,b,c满足题设,由条件①知抛物线的对称轴为x=-1且f(x)min=0;?∴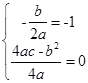 即
即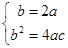 ,所以a=c,在条件②中令x=1,有0≤f(1)-1≤0,?∴f(1)=1,?即a+b+c=1,由
,所以a=c,在条件②中令x=1,有0≤f(1)-1≤0,?∴f(1)=1,?即a+b+c=1,由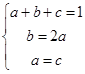 得
得 ,所以存在
,所以存在 使f(x)同时满足条件①②。
使f(x)同时满足条件①②。
考点:本题考查函数的零点与方程根的关系。
点评:本题考查函数零点个数与方程根的个数问题,以及存在性问题的处理方式,属于较难的题目.主要分析思路(1)通过对二次函数对应方程的判别式进行分析判断方程根的个数,从而得到零点的个数;(2)存在性问题的一般处理方法就是假设存在,然后根据题设条件求得参数的值.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
(本小题12分)某公司生产一种产品每年需投入固定成本为0.5万元,此外每生产100件这种产品还需要增加投入0.25万元.经预测知,当售出这种产品 百件时,若
百件时,若 ,则销售所得的收入为
,则销售所得的收入为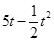 万元:若
万元:若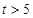 ,则销售收入为
,则销售收入为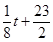 万元.
万元.
(1)若该公司的这种产品的年产量为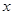 百件
百件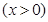 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润 表示为当年生产量
表示为当年生产量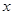 的函数;
的函数;
(2)当年产量为多少时,当年公司所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用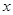 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本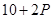 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为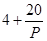 元/万件.
元/万件.
(Ⅰ)将该产品的利润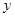 万元表示为促销费用
万元表示为促销费用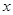 万元的函数;
万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用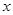 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本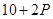 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为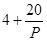 元.
元.
(Ⅰ)将该产品的利润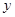 万元表示为促销费用
万元表示为促销费用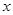 万元的函数(利润=总售价-成本-促销费);
万元的函数(利润=总售价-成本-促销费);
(Ⅱ)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com