
求值:1) ;
;
2)
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)建造一个容积为18立方米,深为2米的长方体有盖水池。如果池底和池壁每平方米的造价分别是200元和150元,那么如何建造,池的造价最低,为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数
(1)若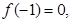 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的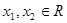 ,且
,且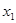 <
<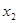 ,
,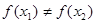 (
(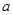 >0),试证明:
>0),试证明: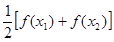 >
>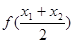 成立。
成立。
(3)是否存在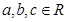 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意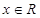 ,
, ,且
,且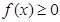 ②对任意的
②对任意的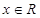 ,都有
,都有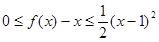 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数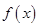 的顶点坐标为
的顶点坐标为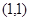 ,且
,且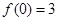 ,
,
(1)求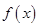 的解析式,
的解析式,
(2)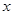 ∈
∈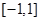 ,
,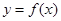 的图象恒在
的图象恒在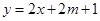 的图象上方,
的图象上方,
试确定实数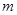 的取值范围,
的取值范围,
(3)若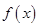 在区间
在区间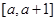 上单调,求实数
上单调,求实数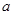 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com