练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分14分）建造一个容积为18立方米，深为2米的长方体有盖水池。如果池底和池壁每平方米的造价分别是200元和150元，那么如何建造，池的造价最低，为多少？

    水池的长、宽都为3米时，水池的造价最低，为7200元

    解析试题分析：设水池的长为米（），宽为米（），总造价为元，             ……1分
    则，即.                                                              ……4分
    由题意得                              ……7分
    ，                                         ……10分
    当且仅当时，取等号.                                                       ……12分
    答：水池的长、宽都为3米时，水池的造价最低，为7200元.                             ……14分
    考点：本小题主要考查利用基本不等式解决实际问题中的最值问题，考查学生利用数学知识解决实际问题的能力和转化问题的能力.
    点评：解决实际应用题时，要注意实际问题中变量的定义域；利用基本不等式求最值时，要交代取等号的条件.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本题满分13分）设函数，且，，求证：（1）且；
    （2）函数在区间内至少有一个零点；
    （3）设是函数的两个零点，则.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）已知二次函数的图象过点（0，—3），且的解集（1，3）。
    （1）求的解析式；
    （2）若当时，恒有求实数t的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分10分）
    已知奇函数
    （1）求实数m的值，并在给出的直角坐标系中画出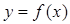的图象；
    （2）若函数在区间[－1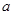，－2]上单调递增，试确定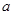的取值范围.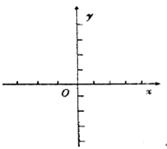

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）已知函数在点处取得极小值－4，使其导函数的的取值范围为（1，3）
    （Ⅰ）求的解析式及的极大值；
    （Ⅱ）当时，求的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数 定义在上，对于任意实数，恒有，且当时，
    （1）求证：,且当时，
    （2）求在上的单调性.
    （3）设集合，，且，
    求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝
    (1)求f(f(－2))的值；
    (2)求f(a2＋1)(a∈R)的值；
    (3)当－4≤x<3时，求函数f(x)的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    求值：1）；
    2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （12分）某车间生产一种仪器的固定成本是10000元，每生产一台该仪器需要增加投入100
    元，已知总收入满足函数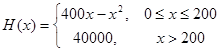：，其中是仪器的月产量.
    （1）将利润表示为月产量的函数（用表示）；
    （2）当月产量为何值时，车间所获利润最大？最大利润是多少元?（总收入＝总成本＋利润）

    查看答案和解析>>

    同步练习册答案