
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100
元,已知总收入满足函数: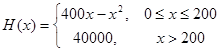 ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(1)将利润表示为月产量的函数(用 表示);
表示);
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?(总收入=总成本+利润)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com