
(本小题两小题,每题6分,满分12分)
⑴对任意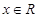 ,试比较
,试比较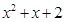 与
与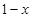 的大小;
的大小;
⑵已知函数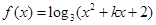 的定义域为R,求实数k的取值范围。
的定义域为R,求实数k的取值范围。
⑴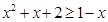 。⑵
。⑵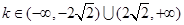
解析试题分析:(1)根据作差法比较大小是一种重要的方法。同时要注意差式的变形技巧的运用。
(2)利用对数函数定义域为R,说明了无论x取什么样的数,表达式真数恒大于零,那么说明二次函数开口向上,判别式小于零得到。
⑴∵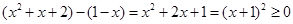 ,∴
,∴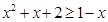 。
。
⑵∵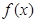 的定义域为
的定义域为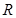 ,即
,即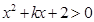 恒成立,∴
恒成立,∴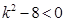 ,
,
即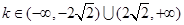
考点:本题主要考查配方法的运用,为判定差是大于零还是小于零,配方法也是常用的方法之一,比差法是比较两个代数式值的大小的常用方法,此题正是有效地利用了这两个方法,使问题得到解决,同时也考查了函数的定义域为R的理解和运用。
点评:解决该试题的关键是要比较两式的大小,可以运用比差法,把两个式子相减,可以得运用配方法来比较与零的大小关系,要使得对数函数定义域为R,说明了对数的真数部分恒大于零。


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
已知二次函数 的最小值为1,且
的最小值为1,且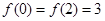 。
。
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间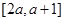 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)在区间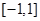 上,
上,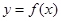 的图象恒在
的图象恒在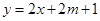 的图象上方,试确定实数
的图象上方,试确定实数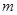 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知奇函数
(1)求实数m的值,并在给出的直角坐标系中画出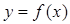 的图象;
的图象;
(2)若函数 在区间[-1,
在区间[-1,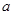 -2]上单调递增,试确定
-2]上单调递增,试确定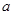 的取值范围.
的取值范围.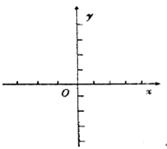
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com