
(本小题满分12分)定义在实数R上的函数y= f(x)是偶函数,当x≥0时,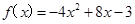 .
.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
(Ⅰ)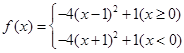 ;(Ⅱ)最大值1,单调递增区间是(-∞,-1
;(Ⅱ)最大值1,单调递增区间是(-∞,-1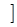 和[0,1] ,单调递减区间是 [-1,0]和[1,+∞
和[0,1] ,单调递减区间是 [-1,0]和[1,+∞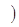 。
。
单调递减区间是 [-1,0]和[1,+∞
解析试题分析:解:(Ⅰ)设x<0,则- x>0, 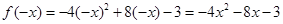
∵f(x)是偶函数,∴f(-x)=f(x) …………… 3
∴x<0时, 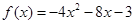
所以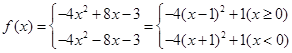 ……………6
……………6
(Ⅱ)y=f(x)开口向下,所以y=f(x)有最大值f(1)=f(-1)=1
函数y=f(x)的单调递增区间是(-∞,-1 和[0,1] …………… 9
和[0,1] …………… 9
单调递减区间是 [-1,0]和[1,+∞ ……………12
……………12
考点:函数的奇偶性;函数的最值;函数的单调性;函数解析式的求法。
点评:利用函数的奇偶性求函数的解析式,这类问题的一般做法是:? ①“求谁设谁”?即求哪个区间上的解析式,x就设在哪个区间内; ②要利用已知区间的解析式进行代入; ③利用f(x)的奇偶性写出-f(x)或f(-x)?从而解出f(x)。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知二次函数 的最小值为1,且
的最小值为1,且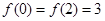 。
。
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间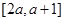 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)在区间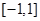 上,
上,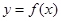 的图象恒在
的图象恒在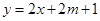 的图象上方,试确定实数
的图象上方,试确定实数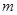 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)设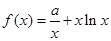 ,
,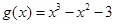 .
.
(1)当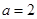 时,求曲线
时,求曲线 在
在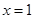 处的切线的斜率;
处的切线的斜率;
(2)如果存在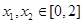 ,使得
,使得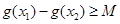 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数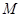 ;
;
(3)如果对于任意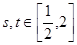 ,都有
,都有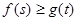 成立,求实数
成立,求实数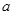 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知奇函数
(1)求实数m的值,并在给出的直角坐标系中画出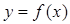 的图象;
的图象;
(2)若函数 在区间[-1,
在区间[-1,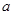 -2]上单调递增,试确定
-2]上单调递增,试确定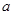 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com