
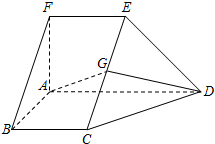
 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,G为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,G为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.分析 (I)由BC∥FE,BC=FE可得四边形BCEF是平行四边形,故而BF∥CE,于是BF∥平面CDE;
(II)过点E作EP⊥AD于P,连接CP、AC、AE,通过计算可得AC=AE=CD=DE,由等腰三角形的性质得出AG⊥CE,DG⊥CE,于是CE⊥平面ADG,故而平面AGD⊥平面CDE;
(III)证明AB⊥平面ADEF,又BF∥CE,于是直线CE与平面ADEF所成角等于BF与平面ADEF所成的角,故∠BFA即为所求的角.
解答 (Ⅰ)证明:∵BC∥FE,BC=FE,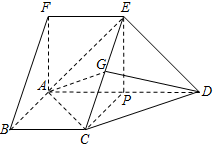
∴四边形BCEF是平行四边形.
∴BF∥CE.
∵BF?平面CDE,CE?平面CDE,
∴BF∥平面CDE.
(Ⅱ)证明:过点E作EP⊥AD于P,连接CP、AC、AE,
设AF=a,则EP=PD=PC=a,AC=AE=$CD=DE=\sqrt{2}a$.
∴△CDE,△ACE为等腰三角形.
∵G为EC的中点,
∴DG⊥CE,AG⊥CE.
又AG?平面ADG,DG?平面ADG,AG∩DG=G,
∴CE⊥平面ADG.
∵CE?平面CDE,
∴平面AGD⊥平面CDE.
(Ⅲ)∵BA⊥AF,BA⊥AD,AF∩AD=A,
∴BA⊥平面ADEF.
∴∠BFA即为直线BF与平面ADEF所成角.
∵$tan∠BFA=\frac{AB}{AF}=1$,
∴∠BFA=45°.
∵BF∥CE,
∴直线CE与平面ADEF所成的角为45°.
点评 本题考查了线面平行,面面垂直的判定,线面角的计算,属于中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | $\frac{16}{3}$π | C. | $\frac{32}{3}$π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
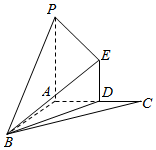 平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 92+14π | B. | 100+10π | C. | 90+12π | D. | 92+10π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{9}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | $\frac{64π}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com