
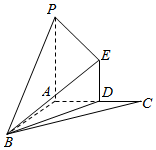
 平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;分析 (1)延长PE交AC于F,可证F与C重合,故直线BC即为面PBE与面ABC的交线;
(2)连接AE,则∠BEA为所要求的角,根据棱锥的体积计算AB,利用勾股定理计算AE,则tan∠BEA=$\frac{AB}{AE}$.
解答 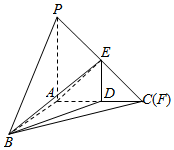 解:(1)延长PE交AC于F
解:(1)延长PE交AC于F
∵AP、AB、AC两两互相垂直,∴PA⊥平面ABC,
∵DE⊥平面ABC,
∴DE∥PA,
∴$\frac{DF}{AF}=\frac{DE}{PA}=\frac{1}{2}$,
∴F与C重合.
∵C∈PE,C∈AC,PE?平面PBE,AC?平面ABC,
∴C是平面PBE和平面ABC的公共点,
又B是平面PBE和平面ABC的公共点,
∴BC是面PBE与面ABC的交线.
(2)连接AE,
∵AP、AB、AC两两互相垂直,
∴AB⊥平面PAC,∴∠BEA为BE与平面PAD所成的角,
∴VB-PADE=$\frac{1}{3}{S}_{梯形ADEP}•AB$=$\frac{1}{3}×\frac{1}{2}×$(1+2)×1×AB=$\frac{\sqrt{3}}{3}$,
∴AB=$\frac{2\sqrt{3}}{3}$.
又∵AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{2}$,
∴tan∠BEA=$\frac{AB}{AE}$=$\frac{\sqrt{6}}{3}$.
∴BE与面PADE所成的线面角为arctan$\frac{\sqrt{6}}{3}$.
点评 本题考查了平面的性质,线面角的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图ABCD-A1B1C1D1是边长为1的正方体,S-ABCD是高为l的正四棱锥,若点S,A1,B1,Cl,D1在同一个球面上,则该球的表面积为( )
如图ABCD-A1B1C1D1是边长为1的正方体,S-ABCD是高为l的正四棱锥,若点S,A1,B1,Cl,D1在同一个球面上,则该球的表面积为( )| A. | $\frac{9}{16}π$ | B. | $\frac{25}{16}π$ | C. | $\frac{49}{16}π$ | D. | $\frac{81}{16}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
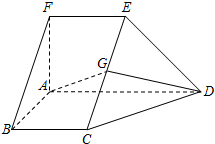 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,G为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,G为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x∈R,x2>0”为真命题 | |
| C. | 命题“若x=y,则cosx=cosy”的逆否命题为真命题 | |
| D. | “p∧q为真命题”是“p∨q为真命题”的必要不充分条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com