
分析 (1)求出过点P,M,N,C2的圆即为以PC2为直径的圆的方程,由此能求出结果.
(3)直线y-y0=k(x-x0)与y轴的交点为(0,y0-kx0),不妨设S(0,y0-k1x0),T(0,y0-k2x0),则ST=|k2-k1|x0=$\frac{\sqrt{4{{x}_{0}}^{2}+4{{y}_{0}}^{2}+8{x}_{0}}}{{x}_{0}+2}$.换元,利用函数的单调性,即可求线段ST长度的取值范围.
解答 解:(1)∵圆C1:(x+1)2+y2=1和圆C2:(x-4)2+y2=4,
∴圆C1:(x+1)2+y2=1的圆心C1(-1,0),半径r1=1,
圆C2:(x-4)2+y2=4的圆心C2(4,0),半径r2=2,
∵过点P(-2,-2)引圆C2的两条割线l1和l2,直线l1和l2被圆C2截得的弦的中点分别为M,N.
∴过点P,M,N,C2的圆即为以PC2为直径的圆的方程,
PC2的中点坐标为(1,-1),|PC2|=$\sqrt{(4+2)^{2}+(0+2)^{2}}$=2$\sqrt{10}$,
∴过点P,M,N,C2的圆的圆心为(1,-1),半径r=$\sqrt{10}$,
直线PC1:$\frac{y+2}{x+2}$=$\frac{-1+2}{0+2}$,即x-2y+2=0,
圆心(1,-1)到直线x-2y=2=0的距离d=$\frac{|1+2+2|}{\sqrt{1+4}}$=$\sqrt{5}$,
∴过点P,M,N,C2的圆被直线PC1所截的弦长为:
2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{10-5}$=2$\sqrt{5}$.
(2)设过Q(x0,y0)的直线与圆C1切线,
则d=$\frac{|-k-k{x}_{0}+{y}_{0}|}{\sqrt{1+{k}^{2}}}$=1,即(k+kx0-y0)2=1+k2,
整理成关于k的方程(x02+2x0)k2-(2y0+2x0y0)k+y02-1=0,(*)
判别式△=(2y0+2x0y0)2-4(y02-1)(x02+2x0)=4x02+4y02+8x0,
∴k=$\frac{2{y}_{0}+2{x}_{0}{y}_{0}±\sqrt{4{{x}_{0}}^{2}+4{{y}_{0}}^{2}+8{x}_{0}}}{2({{x}_{0}}^{2}+2{x}_{0})}$.
直线y-y0=k(x-x0)与y轴的交点为(0,y0-kx0),
不妨设S(0,y0-k1x0),T(0,y0-k2x0),则ST=|k2-k1|x0.
而k1,k2是(*)方程的两根,
则ST=|k2-k1|x0=$\frac{\sqrt{4{{x}_{0}}^{2}+4{{y}_{0}}^{2}+8{x}_{0}}}{{x}_{0}+2}$.
又(x0-4)2+y02=4,
∴ST=$\frac{\sqrt{4{{x}_{0}}^{2}+4{{y}_{0}}^{2}+8{x}_{0}}}{{x}_{0}+2}$=$\frac{\sqrt{40{x}_{0}-48}}{{x}_{0}+2}$=$2\sqrt{2}•\frac{\sqrt{5{x}_{0}-6}}{{x}_{0}+2}$.
令$\sqrt{5{x}_{0}-6}$=t(t∈[2,2$\sqrt{6}$]),则ST=2 $\sqrt{2}$•$\frac{5t}{16+{t}^{2}}$=$\frac{10\sqrt{2}}{t+\frac{16}{t}}$,
考察关于t的函数f(t)=t+$\frac{16}{t}$(t∈[2,2$\sqrt{6}$]),函数f(t)在区间[2.4]是单调递减,在区间[4,2$\sqrt{6}$]上单调递增,
∴(f(t))max=10,(f(t))min=8.
∴ST∈[$\sqrt{2}$,$\frac{5\sqrt{2}}{4}$].
点评 直线和圆的方程的应用,通常要利用垂径定理,研究线段长的取值范围,通常利用函数的单调性.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
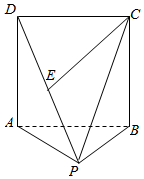 如图,P为正方体ABCD外一点,PB⊥平面ABCD,PB=AB=2,E为PD中点
如图,P为正方体ABCD外一点,PB⊥平面ABCD,PB=AB=2,E为PD中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | $\frac{16}{3}$π | C. | $\frac{32}{3}$π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
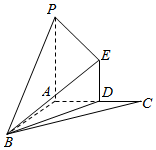 平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com