
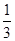 ,a2+a5=4,an=33,则n为( )
,a2+a5=4,an=33,则n为( )| A.50 | B.49 |
| C.48 | D.47 |
科目:高中数学 来源:不详 题型:解答题
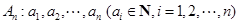 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列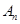 变换成数列
变换成数列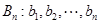 ,其中
,其中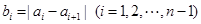 ,且
,且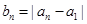 ,这种“
,这种“ 变换”记作
变换”记作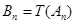 .继续对数列
.继续对数列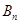 进行“
进行“ 变换”,得到数列
变换”,得到数列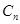 ,…,依此类推,当得到的数列各项均为
,…,依此类推,当得到的数列各项均为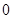 时变换结束.
时变换结束.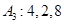 和
和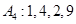 经过不断的“
经过不断的“ 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“ 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;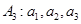 经过有限次“
经过有限次“ 变换”后能够结束的充要条件;
变换”后能够结束的充要条件;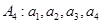 一定能经过有限次“
一定能经过有限次“ 变换”后结束.
变换”后结束.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
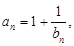 记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明:
记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明: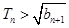
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
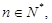 用含有n的代数式表示)
用含有n的代数式表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com