
分析 (1)根据相互独立事件的概率乘法公式和加法公式计算即可,
(2)根据古典概率公式计算即可.
解答 解:(1)设A表示甲命中目标,B表示乙命中目标,则A、B相互独立,
且P(A)=$\frac{1}{3}$,P(B)=$\frac{1}{2}$,
两人恰好各命中一次的概率P=P(A)P(B)+P($\overline{A}$)P(B)+P(A)P($\overline{B}$)=$\frac{1}{3}×\frac{1}{2}$+$\frac{2}{3}×\frac{1}{2}$+$\frac{1}{3}×\frac{1}{2}$=$\frac{2}{3}$,
(2)两人击中目标的总次数大于2,则为甲击中2次,乙击中1次,或甲击中1次,乙击中2次,甲击中2次,乙击中2次,
每人射击两次的基本事件有,设1表示中,0表示不中,基本事件有0000,1000,0100,0010,0001,1100,1010,1001,0011,1110,1101,1011,0111,1111,共14种,其中两人击中目标的总次数大于2的有5种,
故两人击中目标的总次数大于2的概率为$\frac{5}{14}$.
点评 本小题主要考查相互独立事件概率的计算以及古典概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
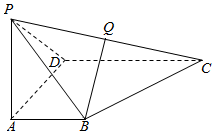 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
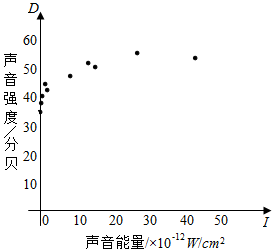 噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{I}$ | $\overline{D}$ | $\overline{W}$ | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)2 | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)2 | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)(Di-$\overline{D}$) | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)(Di-$\overline{D}$) |
| 1.04×10-11 | 45.7 | -11.5 | 1.56×10-21 | 0.51 | 6.88×10-11 | 5.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
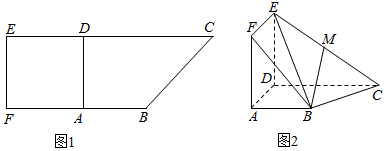
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35种 | B. | 24种 | C. | 18种 | D. | 9种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com