
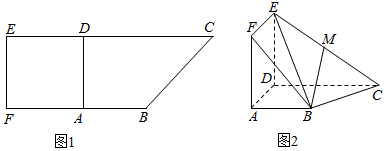
分析 (1)根据面面平行的性质定理即可证明BM∥平面ADEF;
(2)根据二面角的定义作出二面角的平面角进行求解即可.
解答 (1)证明:∵EF=$\frac{1}{2}$BF=$\frac{1}{3}$CE,
∴CE=3EF,BF=2BF,
则AB=AF,CD=2EF,
∵ED=$\frac{1}{3}$EC,
∴ED=EF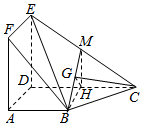
则CD=2AB,
取CD的中点H,连接MH,BH,
则MH是△CDE的中位线,则MH∥DE,
四边形ABHD是正方形,
则BH∥AD,
∵MH∩BH=H,
∴平面BMH∥平面ADEF,
∵BM?平面平面BMH,
∴BM∥平面ADEF;
(2)∵平面ADEF⊥平面ABCD,平面BMH∥平面ADEF,
∴平面BMH⊥平面ABCD,
过H作GH⊥BM,连接CG,
则CG⊥GH,
即∠CGH是平面BMH与平面BEC所成的二面角,同时也是平面ADEF与平面BEC所成的角,
设EF=1,则DE=1,MH=$\frac{1}{2}$,BH=AD=1,CH=1,
则BM=$\sqrt{M{H}^{2}+B{H}^{2}}$=$\sqrt{(\frac{1}{2})^{2}+1}$=$\frac{\sqrt{5}}{2}$,
则$\frac{1}{2}$MH•BH=$\frac{1}{2}$BM•GH,
则GH=$\frac{MH•BH}{BM}$=$\frac{\frac{1}{2}×1}{\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{5}}{5}$,CG=$\sqrt{C{H}^{2}+G{H}^{2}}$=$\sqrt{1+(\frac{\sqrt{5}}{5})^{2}}$=$\frac{\sqrt{30}}{5}$,
则cos∠CGH=$\frac{GH}{CG}$=$\frac{\frac{\sqrt{5}}{5}}{\frac{\sqrt{30}}{5}}$=$\frac{\sqrt{6}}{6}$,
即平面ADEF与平面BEC所成的锐二面角的余弦值是$\frac{\sqrt{6}}{6}$.
点评 本题主要考查线面平行的判定以及二面角的计算,根据二面角的定义作出二面角的平面角是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 26 | C. | 560 | D. | 230 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
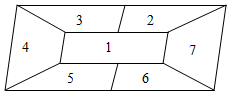 巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.
巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,某地有南北街道5条,东西街道6条,一邮电员从该地东北角的邮局A出发,送信到西南角的B地,且经过C地,要求所走的路程最短,共有多少种不同的走法?
如图所示,某地有南北街道5条,东西街道6条,一邮电员从该地东北角的邮局A出发,送信到西南角的B地,且经过C地,要求所走的路程最短,共有多少种不同的走法?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com