
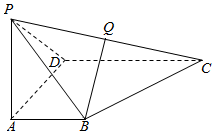
 ��ͼ���ı���ABCD��ֱ�����Σ�AB��CD����ADC=��DAB=90�㣬CD=2AB��PA��ƽ��ABCD��PA=AB=AD��Q��PC���е㣮
��ͼ���ı���ABCD��ֱ�����Σ�AB��CD����ADC=��DAB=90�㣬CD=2AB��PA��ƽ��ABCD��PA=AB=AD��Q��PC���е㣮���� ��1��ȡPD���е�F������AF��FQ���Ƶ����ı���ABQFΪƽ���ı��Σ��ɴ���֤��BQ��ƽ��PAD��
��2�����BQ��ƽ����ƽ��PCD����QE��EΪ��PCD�ı���ƽ����Ľ��㣬��EΪCD���е�ʱ��������Q-BCE���ĸ��涼��ֱ�������Σ�BQ����PCD��BQ��QE��BQ��QC����EQC�ǽ������ƽ��QBC���ɶ���ǵ�ƽ��ǣ��ɴ������ƽ��PBC��ƽ������������ǵ�����ֵ��
��� 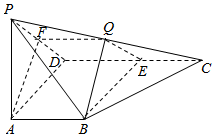 ֤������1��ȡPD���е�F������AF��FQ
֤������1��ȡPD���е�F������AF��FQ
��QΪPC���е㣬��FQΪ��PCD����λ�ߣ�
��FQ��CD����FQ=$\frac{1}{2}$CD��
�֡�AB��CD����AB=$\frac{1}{2}$CD����FQ��AB����FQ=AB��
���ı���ABQFΪƽ���ı��Σ�BQ��AF��
�֡�AF?ƽ��PAD��BQ?ƽ��PAD��
��BQ��ƽ��PAD��
��2�����BQ��ƽ����ƽ��PCD����QE��EΪ��PCD�ı���ƽ����Ľ��㣬
��EΪCD���е�ʱ��������Q-BCE���ĸ��涼��ֱ�������Σ�
֤�����£�
�ߵ�EΪCD���е�ʱ����DE��AB����DE=AB�����ı���ABED��ƽ���ı��Σ�
��BE��AD���֡�ADC=90�㣬���BEC=90�㣬
���BECΪֱ�������Σ�
���ڡ�PAD�У�AD=AP��FΪPD���е㣬��AF��PD��
�֡�PA��ƽ��ABCD��CD��ƽ��ABCD�ڣ���PA��CD��
��CD��AD����CD��ƽ��PAD��
���FDC=90�㣬��QE��PD�����CEQ=90�㣬���CEQΪֱ�������Σ�
�֡�AF?��PAD����AF��CD����PD��CD=D����AF����PCD��
��BQ��AF����BQ����PCD����CQ��EQ����ƽ��PCD�ڣ�
��BQ��CQ��BQ��EQ��
��������Q-BCE���ĸ��涼Ϊֱ�������Σ�
��BQ����PCD��BQ��QE��BQ��QC��
���EQC�ǽ������ƽ��QBC���ɶ���ǵ�ƽ��ǣ�
��PA=AB=AD=1����PD=$\sqrt{2}$��QE=$\frac{\sqrt{2}}{2}$��PC=$\sqrt{6}$��CQ=$\frac{\sqrt{6}}{2}$��
��Rt��QEC��cos��EQC=$\frac{EQ}{QC}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{3}}{3}$��
��ƽ��PBC��ƽ������������ǵ�����ֵΪ$\frac{\sqrt{3}}{3}$��
���� ���⿼������ƽ�е�֤������������������ƽ���Ƿ���ڵ�̽���������е��⣬����ʱҪ�������⣬ע��ռ�˼ά������������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{3}^{3}}$A${\;}_{4}^{4}$ | B�� | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$34 | ||
| C�� | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{4}^{4}}$43 | D�� | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$43 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 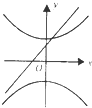 | C�� | 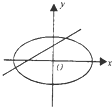 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com