
分析 联立直线y=$\sqrt{11}$x和椭圆方程,求得A,B的坐标,以及|OA|2,将直线OP方程为$x=-\sqrt{11}y$,代入椭圆方程,求得P的坐标及|OP|2,再由|OP|2=3|OA|2,结合离心率公式,可得e.
解答 解:因为$\left\{\begin{array}{l}y=\sqrt{11}x\\{b^2}{x^2}+{a^2}{y^2}={a^2}{b^2}\end{array}\right.⇒{x^2}=\frac{{{a^2}{b^2}}}{{11{a^2}+{b^2}}},{y^2}=\frac{{11{a^2}{b^2}}}{{11{a^2}+{b^2}}}$,
所以${|{OA}|^2}=\frac{{12{a^2}{b^2}}}{{11{a^2}+{b^2}}}$;
由题设直线OP方程为$x=-\sqrt{11}y$,
所以$\left\{\begin{array}{l}x=\sqrt{11}y\\{b^2}{x^2}+{a^2}{y^2}={a^2}{b^2}\end{array}\right.⇒{y^2}=\frac{{{a^2}{b^2}}}{{{a^2}+11{b^2}}},{x^2}=\frac{{11{a^2}{b^2}}}{{{a^2}+11{b^2}}}$,
所以${|{OP}|^2}=\frac{{12{a^2}{b^2}}}{{{a^2}+11{b^2}}}$,
所以$\frac{{{{|{OP}|}^2}}}{{{{|{OA}|}^2}}}=\frac{{11{a^2}+{b^2}}}{{{a^2}+11{b^2}}}=3⇒\frac{{12-{e^2}}}{{12-11{e^2}}}=3⇒e=\frac{{\sqrt{3}}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的对称性和等边三角形的性质,考查化简整理的运算能力,属于中档题.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
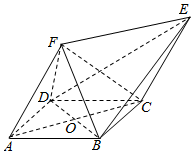 如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.
如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosα≠0是α≠2kπ+$\frac{π}{2}$(k∈Z)的充分必要条件 | |
| B. | 函数f(x)=3ln|x|的零点是(1,0)和(-1,0) | |
| C. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=$\frac{1}{2}$-p | |
| D. | 若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差会改变 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
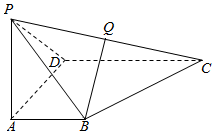 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com