
| A. |  | B. | 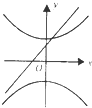 | C. | 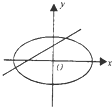 | D. | 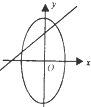 |
分析 根据题意,可以整理方程ax+by+c=0和ax2+by2=1变形为斜截式和标准形式,可以判断其形状,进而分析直线所在的位置可得答案.
解答 解:方程ax+by+c=0化成:y=-$\frac{a}{b}$x-$\frac{c}{b}$,ax2+by2=1化成:$\frac{{x}^{2}}{\frac{1}{a}}+\frac{{y}^{2}}{\frac{1}{b}}=1$,
对于A:由双曲线图可知:a>0,b<0,∴-$\frac{a}{b}$>0,即直线的斜率大于0,故错;
对于B:由双曲线图可知:b>0,a<0,∴-$\frac{a}{b}$>0,即直线的斜率大于0,截距为正数,故B正确;
对于C:由椭圆图可知:b>0,a>0,∴-$\frac{a}{b}$<0,即直线的斜率小于0,故错;
对于D:由椭圆图可知:b>0,a>0,∴-$\frac{a}{b}$<0,即直线的斜率小于0,故错;
故选:B.
点评 本题考查由椭圆、双曲线、直线的方程判断图象的方法,注意先判断曲线的形状,再分析大致等位置.属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| (x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
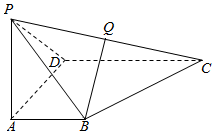 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{e}$,+∞) | B. | (0,$\frac{1}{e}$) | C. | (-$\frac{1}{e}$,+∞) | D. | (-$\frac{1}{e}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
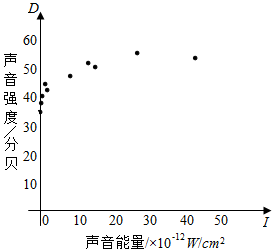 噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{I}$ | $\overline{D}$ | $\overline{W}$ | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)2 | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)2 | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)(Di-$\overline{D}$) | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)(Di-$\overline{D}$) |
| 1.04×10-11 | 45.7 | -11.5 | 1.56×10-21 | 0.51 | 6.88×10-11 | 5.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35种 | B. | 24种 | C. | 18种 | D. | 9种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com