
| A. | ($\frac{1}{e}$,+∞) | B. | (0,$\frac{1}{e}$) | C. | (-$\frac{1}{e}$,+∞) | D. | (-$\frac{1}{e}$,0) |
分析 利用函数与方程的关系,利用参数分离法进行分离,构造函数,求出函数的导函数,求出函数的最小值,根据函数的零点和最值关系即可得到结论.
解答 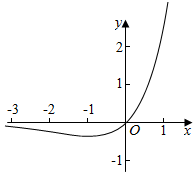 解:若f(x)=xex-a有两个零点,等价为f(x)=xex-a=0,即a=xex有两个根,
解:若f(x)=xex-a有两个零点,等价为f(x)=xex-a=0,即a=xex有两个根,
设h(x)=xex,
则函数h(x)=xex的导函数h′(x)=(x+1)ex,
令h′(x)=0,则x=-1
∵当x∈(-∞,-1)时,h′(x)<0,函数f(x)单调递减;
当x∈(-1,+∞)时,h′(x)>0,函数f(x)单调递增;
故当x=-1时,函数取最小值h(-1)=-e-1,
∵当x≥0时,h(x)≥0,
当x<0时,h(x)<0,
∴若a=xex有两个根,
则$-\frac{1}{e}$<a<0,
故选:D
点评 本题考查的知识点是根的存在性及根的个数判断,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键,利用导数是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | l | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,$\sqrt{5}$) | C. | (0,2$\sqrt{5}$) | D. | (0,10) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
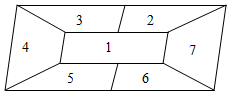 巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.
巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com