
���� ��I������ƽ�����������������㣬���Ǻ�����ȱ任��Ӧ�û���������ʽ�ɵ�f��x��=$2sin��2x-\frac{��}{6}��$���������Ǻ��������ڹ�ʽ���ɵý⣮
��II���ɣ�I��֪�ɵ�$sin��2A-\frac{��}{6}��=1$�����A�ķ�Χ����$A=\frac{��}{3}$���ⷨһ�������Ҷ������c��ֵ���ⷨ���������Ҷ������sinB����B����ǣ�����cosB�������������ڽǺͶ��������Ǻ͵����Һ�����ʽ����sinC���������Ҷ������ɽ��c��ֵ��
��� �⣺��I��f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$+2=$2sinx��sinx+\sqrt{3}cosx��-3+2$����2�֣�
=$2{sin^2}x+2\sqrt{3}sinxcosx-1$
=$\sqrt{3}sin2x-cos2x$����4�֣�
=$2sin��2x-\frac{��}{6}��$����5�֣�
��f��x������С������$T=\frac{2��}{2}=��$����6�֣�
��II���ɣ�I��֪$f��A��=2sin��2A-\frac{��}{6}��=2$�����$sin��2A-\frac{��}{6}��=1$������7�֣�
��$A�ʣ�{0��\frac{��}{2}}����\;��2A-\frac{��}{6}�ʣ�{-\frac{��}{6}��\frac{5��}{6}}��$��
��$2A-\frac{��}{6}=\frac{��}{2}$����$A=\frac{��}{3}$������9�֣�
�ⷨһ�������Ҷ�����${a^2}={3^2}+{c^2}-2��3c��cos\frac{��}{3}$=c2-3c+9=7��
���c=1��c=2������10�֣�
��c=1����$cosB=\frac{{{1^2}+{{��{\sqrt{7}}��}^2}-{3^2}}}{{2��1��\sqrt{7}}}$��0��
��BΪ�۽ǣ������ABCΪ��������β�����c��1������11�֣�
��c=2������12�֣�
�ⷨ���������Ҷ�����$\frac{3}{sinB}=\frac{{\sqrt{7}}}{{sin\frac{��}{3}}}$�����$sinB=\frac{{3\sqrt{21}}}{14}$����10�֣�
��B����ǣ���$cosB=\sqrt{1-{{sin}^2}B}=\frac{{\sqrt{7}}}{14}$��
��C=��-��A+B����
��$sinC=sin��A+B��=sin��\frac{��}{3}+B��=\frac{{\sqrt{21}}}{7}$������11�֣�
��$\frac{c}{{\frac{{\sqrt{21}}}{7}}}=\frac{{\sqrt{7}}}{{\frac{{\sqrt{3}}}{2}}}$�����c=2������12�֣�
���� ������Ҫ������ƽ�����������������㣬���Ǻ�����ȱ任��Ӧ�ã����Ǻ��������ڹ�ʽ�����Ҷ��������Ҷ������������ڽǺͶ��������Ǻ͵����Һ�����ʽ�ڽ��������е�Ӧ�ã�������ת��˼������ν��˼���Ӧ�ã������˼��������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��1] | B�� | [0��+�ޣ� | C�� | ��0��1�� | D�� | [0��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 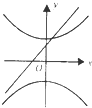 | C�� | 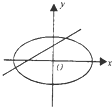 | D�� | 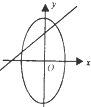 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��0��$\sqrt{5}$�� | C�� | ��0��2$\sqrt{5}$�� | D�� | ��0��10�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com