
| ��Ա��� | 1 | 2 | 3 | 4 | 5 |
| ��x��y��z�� | ��1��1��2�� | ��2��1��1�� | ��2��2��2�� | ��0��1��1�� | ��1��2��1�� |
| ��Ա��� | 6 | 7 | 8 | 9 | 10 |
| ��x��y��z�� | ��1��2��2�� | ��1��1��1�� | ��1��2��2�� | ��1��0��0�� | ��1��1��1�� |
���� �����¼�AΪ����10������������ȡ���ˣ������˵ľ�ס�����ָ��z��ͬ������10������������ȡ���ˣ�����������¼�����������������˵ľ�ס�����ָ��z��ͬ�Ľ�����ɴ�����������˵ľ�ס�����ָ��z��ͬ�ĸ��ʣ�
�����������=m-n�Ŀ���ȡֵΪ1��2��3��4��5���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к�E�Σ�
��� �⣺�����¼�AΪ����10������������ȡ���ˣ������˵ľ�ס�����ָ��z��ͬ����
���ס����ָ��zΪ0��ֻ�б��Ϊ9��һλ��
��ס����ָ��zΪ1���б��Ϊ2��4��5��7��10������λ��
��ס����ָ��zΪ2���б��Ϊ1��3��6��8������λ��
��10������������ȡ���ˣ������¼�����n=${C}_{5}^{2}$=10��
�����˵ľ�ס�����ָ��z��ͬ�Ľ��Ϊ${C}_{5}^{2}+{C}_{4}^{2}$=16��
�������˵ľ�ס�����ָ��z��ͬ�ĸ���p=$\frac{16}{45}$��
������10���������ߵ��ۺ�ָ�꣬�����±���
| ��Ա��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| �ۺ�ָ�� | 4 | 4 | 6 | 2 | 4 | 5 | 3 | 5 | 1 | 3 |
| �� | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{4}$ | $\frac{7}{24}$ | $\frac{7}{24}$ | $\frac{1}{8}$ | $\frac{1}{24}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{��}{2}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{4}{3}$ | C�� | l | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��1] | B�� | [0��+�ޣ� | C�� | ��0��1�� | D�� | [0��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{3}^{3}}$A${\;}_{4}^{4}$ | B�� | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$34 | ||
| C�� | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{4}^{4}}$43 | D�� | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$43 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 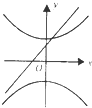 | C�� | 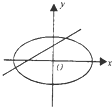 | D�� | 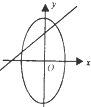 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com