练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若α是第一象限角，则sinα+cosα的值与1的大小关系是（ ）

    A. sinα+cosα＞1B. sinα+cosα=1C. sinα+cosα＜1D. 不能确定

    【答案】A

    【解析】

    试题设角α的终边为OP，P是角α的终边与单位圆的交点，PM垂直于x轴，M为垂足，则由任意角的三角函数的定义，可得sinα=MP=|MP|，cosα=OM=|OM|，再由三角形任意两边之和大于第三边，得出结论．

    解：如图所示：设角α的终边为OP，P是角α的终边与单位圆的交点，PM垂直于x轴，M为垂足，则由任意角的三角函数的定义，

    可得sinα=MP=|MP|，cosα=OM=|OM|．△OPM中，∵|MP|+|OM|＞|OP|=1，∴sinα+cosα＞1，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的公比为q，记bn=am（n﹣1）+1+am（n﹣1）+2+…+am（n﹣1）+m ， cn=am（n﹣1）+1am（n﹣1）+2…am（n﹣1）+m ， （m，n∈N*），则以下结论一定正确的是（ ）
    A.数列{bn}为等差数列，公差为qm
    B.数列{bn}为等比数列，公比为q2m
    C.数列{cn}为等比数列，公比为
    D.数列{cn}为等比数列，公比为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AA1=1，AB=3k，AD=4k，BC=5k，DC=6k，（k＞0）

    （1）求证：CD⊥平面ADD1A1
    （2）若直线AA1与平面AB1C所成角的正弦值为 ，求k的值
    （3）现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成的新四棱柱中，记其中最小的表面积为f（k），写出f（k）的解析式．（直接写出答案，不必说明理由）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a=3，b=2 ，∠B=2∠A．
    （1）求cosA的值；
    （2）求c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．

    （1）求证：AA1⊥平面ABC；
    （2）求证二面角A1﹣BC1﹣B1的余弦值；
    （3）证明：在线段BC1上存在点D，使得AD⊥A1B，并求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形是正方形，平面,分别是线段的中点，.

    (1)证明：平面；

    (2)设点是线段的中点，求二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，O是坐标原点，两定点A，B满足| |=| |= =2，则点集{P| =λ +μ ，|λ|+|μ|≤1，λ，μ∈R}所表示的区域的面积是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的通项公式为an＝则数列{an}中的最大项为(　　)

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移1个单位长度，得到的图象是（ ）
    A.
    B.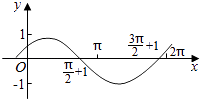
    C.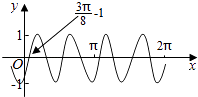
    D.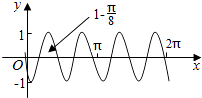

    查看答案和解析>>

    同步练习册答案