
分析 将(1,2)代入直线方程,求得$\frac{1}{a}$+$\frac{2}{b}$=1,利用“1”代换,根据基本不等式的性质,即可求得2a+b的最小值.
解答 解:直线$\frac{x}{a}+\frac{y}{b}$=1(a>0,b>0)过点(1,2),则$\frac{1}{a}$+$\frac{2}{b}$=1,
由2a+b=(2a+b)×($\frac{1}{a}$+$\frac{2}{b}$)=2+$\frac{4a}{b}$+$\frac{b}{a}$+2=4+$\frac{4a}{b}$+$\frac{b}{a}$≥4+2$\sqrt{\frac{4a}{b}×\frac{b}{a}}$=4+4=8,
当且仅当$\frac{4a}{b}$=$\frac{b}{a}$,即a=$\frac{1}{2}$,b=1时,取等号,
∴2a+b的最小值为8,
故答案为:8.
点评 本题考查基本不等式的应用,考查“1”代换,考查计算能力,属于基础题.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
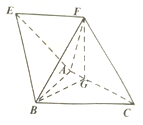 如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
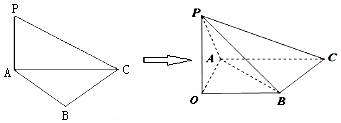
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
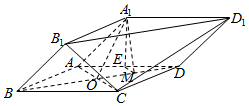 由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,
由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,2) | C. | (1,$\sqrt{2}$) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {1,4} | C. | {1,2,3,4,6,7,9} | D. | {2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com