
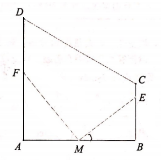
 ij��ֳ��ԭ��һ��ֱ�����ε�ˮ��ABCD������BC��AD���AB��ֱ��AD=800m��AB=2BC=600m��Ϊ������㰮������Ҫ���ƻ����������ഹֱ��ˮ��ջ��MF��ME����M��E��F���ڰ����ϣ�����MΪAB���е㣬��E�ڰ���BC�ϣ����EMB=��rad��ˮ��ջ��MF��ME�ij��Ⱥͼ�Ϊf���ȣ�����λ��m����
ij��ֳ��ԭ��һ��ֱ�����ε�ˮ��ABCD������BC��AD���AB��ֱ��AD=800m��AB=2BC=600m��Ϊ������㰮������Ҫ���ƻ����������ഹֱ��ˮ��ջ��MF��ME����M��E��F���ڰ����ϣ�����MΪAB���е㣬��E�ڰ���BC�ϣ����EMB=��rad��ˮ��ջ��MF��ME�ij��Ⱥͼ�Ϊf���ȣ�����λ��m�������� ��1����E��BC�ϣ���EMB=�ȣ��ó�0���ȡ�45�㣻
����ֱ�������εı߽ǹ�ϵ���ME��MF��д��f���ȣ�=ME+MF��
��2�����f���ȣ��ĵ���������f�䣨�ȣ�=0���f���ȣ�����Сֵ�Լ���Ӧ�Ħ�ֵ��
��� �⣺��1������ABCD�У�BC��AB��AD��BC��AD=800m��AB=2BC=600m��
MF��ME����MΪAB���е㣬��E��BC�ϣ����EMB=�ȣ���0���ȡ�45�㣻
��ME=$\frac{MB}{cos��}$=$\frac{300}{cos��}$��
MF=$\frac{MA}{cos��90��-�ȣ�}$=$\frac{300}{sin��}$��
��f���ȣ�=$\frac{300}{cos��}$+$\frac{300}{sin��}$������0�㣼�ȡ�45�㣬
��0��tan�ȡ�1��
��2����f���ȣ�=$\frac{300}{cos��}$+$\frac{300}{sin��}$��
��f�䣨�ȣ�=300��$\frac{sin��}{{cos}^{2}��}$-$\frac{cos��}{{sin}^{2}��}$��=300•$\frac{{sin}^{3}��{-cos}^{3}��}{{sin}^{2}{��cos}^{2}��}$��
��f�䣨�ȣ�=0�����sin��=cos�ȣ�
���=45�㣬��0�㣼�ȣ�45��ʱ��f�䣨�ȣ���0��f���ȣ������ݼ���
���=45��ʱ��f���ȣ�=$\frac{300}{\frac{\sqrt{2}}{2}}$+$\frac{300}{\frac{\sqrt{2}}{2}}$=600$\sqrt{2}$��Ϊ��Сֵ��
���� ���⿼����ֱ�������α߽ǹ�ϵ��Ӧ�����⣬Ҳ���������Ǻ�������ֵ���⣬���ۺ�����Ŀ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCDΪ���Σ�AB��CD��PD��ƽ��ABCD����BAD=��ADC=90�㣬$DC=2AB=2��DA=\sqrt{3}$��
��ͼ���ı���ABCDΪ���Σ�AB��CD��PD��ƽ��ABCD����BAD=��ADC=90�㣬$DC=2AB=2��DA=\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2} | B�� | {2��3} | C�� | {1��2��3} | D�� | {0��1��2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 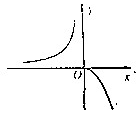 | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��-2�� | B�� | ��-1��2�� | C�� | ��1��2�� | D�� | ��-1��-2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com