
分析 先根据两角和公式对函数解析式进行化简,再根据正弦函数的性质得出答案.
解答 解:y=sinx-cosx=$\sqrt{2}$($\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx)=$\sqrt{2}$(sinxcos$\frac{π}{4}$-cosxsin$\frac{π}{4}$)=$\sqrt{2}$sin(x-$\frac{π}{4}$),
∵x∈[$\frac{π}{2}$,$\frac{3π}{4}$],
∴x-$\frac{π}{4}$∈[$\frac{π}{4}$,π],
∴sin(x-$\frac{π}{4}$)∈[0,1],
∴$\sqrt{2}$sin(x-$\frac{π}{4}$)∈[0,$\sqrt{2}$],即函数的值域为[0,$\sqrt{2}$],
故答案为:[0,$\sqrt{2}$].
点评 本题主要考查两角和公式及三角函数值域问题.把三角函数化简成y=Asin(ωx+φ)的形式很关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
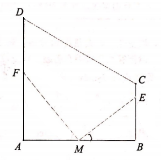 某养殖场原有一块直角梯形的水域ABCD,其中BC,AD与边AB垂直,AD=800m,AB=2BC=600m.为满足钓鱼爱好者需要,计划修建两道互相垂直的水上栈道MF与ME,点M,E,F都在岸边上,其中M为AB的中点,点E在岸边BC上,设∠EMB=θrad,水上栈道MF与ME的长度和记为f(θ)(单位:m).
某养殖场原有一块直角梯形的水域ABCD,其中BC,AD与边AB垂直,AD=800m,AB=2BC=600m.为满足钓鱼爱好者需要,计划修建两道互相垂直的水上栈道MF与ME,点M,E,F都在岸边上,其中M为AB的中点,点E在岸边BC上,设∠EMB=θrad,水上栈道MF与ME的长度和记为f(θ)(单位:m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com