
分析 (Ⅰ)由已知等式求出公差,然后求通项公式;
(Ⅱ)由(Ⅰ)化简得到数列{cn}的通项公式,利用分组求和得到所求.
解答 解:(Ⅰ)等差数列{an}中,a1=3,a2+a5=11=a1+a6.
所以a6=8,所以公差为1,所以an=n+2;
(Ⅱ)所以cn=2${\;}^{{a}_{n}-2}$+n=2n+n,
所以数列{cn}的前10项和S10=(1+2+…+10)+(2+22+23+…+210)=$\frac{10×11}{2}+\frac{2×(1-{2}^{10})}{1-2}$=55-2+211=53+211.
点评 本题考查了等差数列的通项公式以及对数列分组求和;属于常规题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)=x2 | B. | $g(x)=\frac{1}{x}$ | C. | g(x)=x3 | D. | $g(x)={x^{\frac{1}{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
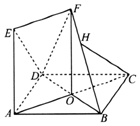 如图,正方形ABCD的对角线AC与BD相交于点O,四边形OAEF为矩形,平面OAEF⊥平面ABCD,AB=AE.
如图,正方形ABCD的对角线AC与BD相交于点O,四边形OAEF为矩形,平面OAEF⊥平面ABCD,AB=AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\sqrt{5},+∞})$ | C. | $({\frac{{\sqrt{5}}}{2},\sqrt{5}})$ | D. | $({1,\frac{{\sqrt{5}}}{2}})∪({\sqrt{5},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
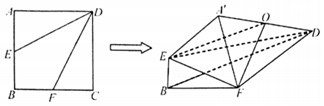
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,$DC=2AB=2,DA=\sqrt{3}$.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,$DC=2AB=2,DA=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R,$x_0^2+{x_0}+1≥0$ | B. | ?x0∈R,$x_0^2+{x_0}+1≥0$ | ||
| C. | ?x∈R,x2+x+1<0 | D. | ?x∈R,x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com