
分析 设事件A表示“抽到的两张都是假钞”,事件B表示“抽到的两张至少有一张假钞”,所求的概率即 P(A/B).先求出P(AB)和P(B)的值,再根据P(A/B)=$\frac{P(AB)}{P(B)}$,运算求得结果.
解答 解:设事件A表示“抽到的两张都是假钞”,事件B表示“抽到的两张至少有一张假钞”,
则所求的概率即 P(A/B).
又P(AB)=P(A)=$\frac{{C}_{4}^{2}}{{C}_{20}^{2}}$,P(B)=$\frac{{C}_{4}^{2}+{C}_{4}^{1}{C}_{16}^{1}}{{C}_{20}^{2}}$,
由公式P(A/B)=$\frac{P(AB)}{P(B)}$=$\frac{{C}_{4}^{2}}{{C}_{4}^{2}+{C}_{4}^{1}{C}_{16}^{1}}$=$\frac{3}{35}$.
故答案为:$\frac{3}{35}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意条件概率的性质的合理运用.


科目:高中数学 来源: 题型:解答题
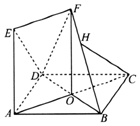 如图,正方形ABCD的对角线AC与BD相交于点O,四边形OAEF为矩形,平面OAEF⊥平面ABCD,AB=AE.
如图,正方形ABCD的对角线AC与BD相交于点O,四边形OAEF为矩形,平面OAEF⊥平面ABCD,AB=AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R,$x_0^2+{x_0}+1≥0$ | B. | ?x0∈R,$x_0^2+{x_0}+1≥0$ | ||
| C. | ?x∈R,x2+x+1<0 | D. | ?x∈R,x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
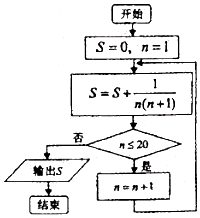
| A. | $\frac{21}{22}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{20}$ | D. | $\frac{22}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,5] | B. | [2,$\frac{7}{2}$] | C. | [$\frac{7}{2}$,5] | D. | [5,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com