Question

2．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，P为双曲线右支上的一点，△POF₁为等腰三角形，过点P作y轴的垂线，延长后交双曲线的左支于点Q，若$\overrightarrow{PQ}$=$\frac{1}{2}$$\overrightarrow{{F}_{2}{F}_{1}}$，则双曲线离心率为$\sqrt{3}$+1．

Answer 1

分析 根据题意，作出双曲线的图象，设|F₁F₂|=2c，则|F₁O|=|F₂O|=c，结合题意分析可得?QF₁OP为菱形，且△POQ为等边三角形，进而分析可得∠OPQ=60°，∠PF₁F₂=30°，即可得|PF₁|=$\sqrt{3}$c，由双曲线的定义可得2a=|PF₁|-|PF₂|=（$\sqrt{3}$-1）c，由双曲线的离心率公式计算可得答案．

解答 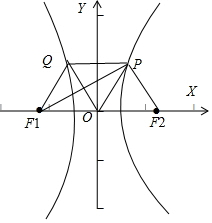解：根据题意，作出双曲线的图象，设|F₁F₂|=2c，
则|F₁O|=|F₂O|=c，
若$\overrightarrow{PQ}$=$\frac{1}{2}$$\overrightarrow{{F}_{2}{F}_{1}}$，则有PQ∥F₁F₂，且|PQ|=$\frac{1}{2}$|F₁F₂|=|F₁O|，
四边形QF₁OP为平行四边形，
又由△POF₁为等腰三角形，则有|OP|=|F₁O|，
故?QF₁OP为菱形，则有|PO|=|PQ|=|F₁O|=|F₁Q|，
又由|PO|=|OQ|，则有△POQ为等边三角形，
即∠OPQ=60°，∠PF₁F₂=30°，
又由∠PF₂O=60°，且|PF₂|=|QF₁|=c，
又由|F₁F₂|=2c，则|PF₁|=$\sqrt{3}$c，
双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1中：2a=|PF₁|-|PF₂|=（$\sqrt{3}$-1）c，
则双曲线的离心率e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1；
故答案为：$\sqrt{3}$+1．

点评 本题考查双曲线的几何性质，注意借助双曲线的对称性分析PO、OQ和F₁Q、F₂P的关系．