练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在类比此性质，如下图，在四面体P－ABC中，若PA、PB、PC两两垂直，底面ABC上的高为h，则得到的正确结论为________________．

    解析试题分析：如图所示，两两垂直，则平面，所以,在直角三角形中有,平面,则,又,故平面,那么,在直角三角形中，,可得.

    考点：线面垂直的判定与性质.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    设是两条不同的直线，是两个不重合的平面，给定下列四个命题：
    ①若，，则；
    ②若，，则；
    ③若，，则；
    ④若，，，则.
    其中真命题的序号为       ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设m,n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题：
    （1）若m⊥α，n∥α，则m⊥n
    （2）若α∥β，β∥γ，m⊥α，则m⊥γ
    （3）若m∥α，n∥α，则m∥n
    （4）若α⊥γ，β⊥γ，则α∥β
    其中真命题的序号是          ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    若P是两条异面直线l、m外的任意一点，则下列命题中假命题的是________．(填序号)
    ①过点P有且仅有一条直线与l、m都平行；
    ②过点P有且仅有一条直线与l、m都垂直；
    ③过点P有且仅有一条直线与l、m都相交；
    ④过点P有且仅有一条直线与l、m都异面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图，在Rt△ABC中，∠ABC=90，PA⊥平面ABC，则四面体P-ABC中共有（   ）个直角三角形

    A．4 B．3 C．2 D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设l，m，n表示不同的直线，α，β，γ表示不同的平面，给出下列四个命题：
    ①若m∥l，且m⊥α，则l⊥α；
    ②若m∥l，且m∥α，则l∥α；
    ③若α∩β＝l，β∩γ＝m，γ∩α＝n，则l∥m∥n；
    ④若α∩β＝m，β∩γ＝l，γ∩α＝n，且n∥β，则l∥m.
    其中正确命题的个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    [2014·长春质检]如图，四棱锥P－ABCD的底面是一直角梯形，AB∥CD，BA⊥AD，CD＝2AB，PA⊥底面ABCD，E为PC的中点，则BE与平面PAD的位置关系为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论：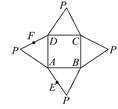

    ①直线BE与直线CF异面;
    ②直线BE与直线AF异面;
    ③直线EF∥平面PBC;
    ④平面BCE⊥平面PAD.
    其中正确的有__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    [2014·汕头质检]一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：

    ①AB⊥EF；
    ②AB与CM所成的角为60°；
    ③EF与MN是异面直线；
    ④MN∥CD.
    以上四个命题中，正确命题的序号是________．

    查看答案和解析>>

    同步练习册答案